Condensador con dos capas de dieléctrico

De Laplace

(Diferencias entre revisiones)

última version al 19:45 18 feb 2011

1 Enunciado

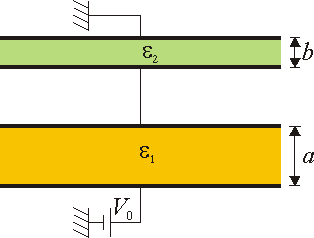
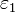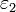Entre dos placas metálicas conductoras planas y paralelas a una distancia $d = a + b$ se colocan dos dieléctricos de permitividades $\varepsilon_1$ y $\varepsilon_2$ y espesores $a$ y $b$ respectivamente, tal como muestra la figura. Halle la capacidad de este condensador y construya el circuito equivalente.

2 Solución

Para obtener la capacidad de un condensador debemos, o bien fijar la carga sobre una de las placas y, a partir de ella obtener la diferencia de potencial entre placas, o fijar esta última y determinar la carga almacenada.

Si elegimos este segundo camino, consideramos que la placa inferior ( $z = 0$ ) se encuentra puesta a tierra, mientras que la superior ( $z = a + b$ ) está a un potencial $V 0$ . Para hallar la carga necesitamos el valor de $\mathbf{D}$ y, por tanto, de $\mathbf{E}$ , en el espacio intermedio.

Al despreciar los efectos de borde, admitimos que el campo es en todo momento perpendicular a las placas, por lo que, en cada región se escribirá

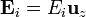
$\mathbf{E}_i=E_i\mathbf{u}_{z}$ $i=1,2\,$

y, por tratarse de medios lineales

$\mathbf{D}_i=\varepsilon_i\mathbf{E}_i=(\varepsilon_iE_i)\mathbf{u}_{z}=D_i\mathbf{u}_z$ $i=1,2\,$

esto es, tanto el campo eléctrico como el vector desplzamiento poseen una única componente no nula.

La condición de que el campo electrostático es irrotacional conduce a que, en cada una de las dos regiones,

$\mathbf{0}=\nabla\times \mathbf{E}_i=\left|\begin{matrix}\mathbf{u}_{x} & \mathbf{u}_{y} & \mathbf{u}_{z} \\ & & \\ \displaystyle\frac{\partial\ }{\partial x} & \displaystyle\frac{\partial\ }{\partial y} & \displaystyle\frac{\partial\ }{\partial z} \\ & & \\ 0 & 0 & E_i\end{matrix}\right|=\frac{\partial E_i}{\partial y}\mathbf{u}_{x}-\frac{\partial E_i}{\partial x}\mathbf{u}_{y}$

y, por tanto,

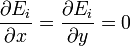
$\frac{\partial{}E_i}{\partial{}x}=\frac{\partial{}E_i}{\partial{}y}=0$

El campo en cada región es independiente de las coordenadas transversales. Sólo dependerá, en todo caso, de la coordenada $z$ .

Por su parte, la ley de Gauss en cada medio establece que

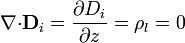
$\nabla{\cdot}\mathbf{D}_i=\frac{\partial{}D_i}{\partial{}z}=\rho_l=0$

por lo que $D i$ no depende de $z$ . Por ser 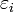$\varepsilon_i$ uniforme, $E i$ tampoco lo hace (compárese este resultado con el del problema de medio estratificado, donde $\mathbf{D}$ no depende de $z$ , pero $\mathbf{E}$ sí).

Por tanto, en cada región, el campo eléctrico es uniforme y va en la dirección $z$ . Sea

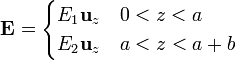
$\mathbf{E}=\begin{cases}E_1\mathbf{u}_{z} & 0<z<a\\ E_2\mathbf{u}_{z} & a<z<a+b\end{cases}$

La condición de que la diferencia de potencial entre placas es $V 0$ conduce a que

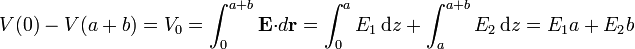
$V(0)-V(a+b)=V_0=\int_0^{a+b}\mathbf{E}{\cdot}d\mathbf{r}= \int_0^aE_1\,\mathrm{d}z+\int_a^{a+b}E_2\,\mathrm{d}z=E_1a+E_2b$

Necesitamos otra ecuación para determinar $E 1$ y $E 2$ .

Ésta sale de las condiciones de contorno en la interfaz que separa los dos dieléctricos. Sobre ella se cumple

$\mathbf{n}{\cdot}[\mathbf{D}]=\sigma_l=0$ $\mathbf{n}\times[\mathbf{E}]=\mathbf{0}$

La segunda condición, sobre las componentes tangenciales del campo eléctrico, se verifica idénticamente, ya que estas son nulas en la interfaz.

La primera que establece que no hay cargas libres en la superficie de separación, conduce a

$\mathbf{n}{\cdot}[\mathbf{D}]=\mathbf{u}_{z}{\cdot}(\mathbf{D}_2-\mathbf{D}_1)=\varepsilon_2E_2-\varepsilon_1E_1=0$

Esta condición se verifica porque suponemos que los dieléctricos son ideales y, por tanto, no hay posibilidad de que la carga libre fluya a través de ellos hasta la interfaz. Si los dieléctricos no fueran ideales, sino que admitieran el paso de una pequeña corriente, entonces sí podría haber carga libre en la interfaz, como se ve en los problemas de corriente eléctrica.

Así pues, tenemos las dos ecuaciones

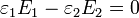
$aE_1+bE_2 = V_0\,$ $\varepsilon_1E_1-\varepsilon_2E_2 = 0\,$

cuya solución es

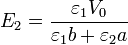
$E_1=\frac{\varepsilon_2V_0}{\varepsilon_1b+\varepsilon_2a}$ $E_2=\frac{\varepsilon_1V_0}{\varepsilon_1b+\varepsilon_2a}$

El campo en cada región posee el sentido de los potenciales decrecientes y es mayor donde la permitividad es menor. El desplazamiento eléctrico, en cambio, posee el mismo valor en todo el espacio entre las placas

$\mathbf{D}=\frac{\varepsilon_1\varepsilon_2V_0}{\varepsilon_1b+\varepsilon_2a}\mathbf{u}_{z}$

Conocido $\mathbf{D}$ podemos hallar la carga sobre una de las placas a partir del flujo de este campo a través de una superficie que envuelva la placa.

Para la placa inferior (la cargada positivamente) el flujo se compone de una parte exterior al condensador (en la cual $\mathbf{D}$ es nulo, ya que se supone que solo hay campos en el interior) y una parte por su interior, en la que la normal va hacia arriba

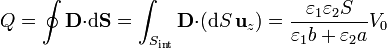
$Q=\oint\mathbf{D}{\cdot}\mathrm{d}\mathbf{S}=\int_{S_\mathrm{int}} \mathbf{D}{\cdot}(\mathrm{d}S\,\mathbf{u}_{z})= \frac{\varepsilon_1\varepsilon_2S}{\varepsilon_1b+\varepsilon_2a}V_0$

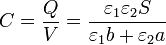
por lo que la capacidad vale $C=\frac{Q}{V}=\frac{\varepsilon_1\varepsilon_2S}{\varepsilon_1b+\varepsilon_2a}$

Esta capacidad verifica que

$\frac{1}{C}=\frac{\varepsilon_1b+\varepsilon_2a}{\varepsilon_1\varepsilon_2S}=\frac{b}{\varepsilon_2S}+\frac{a}{\varepsilon_1S}=\frac{1}{\displaystyle\frac{\varepsilon_2S}{b}}+\frac{1}{\displaystyle\frac{\varepsilon_1S}{a}}=\frac{1}{C_2}+ \frac{1}{C_1}$

esto es, equivale a la de dos condensadores planos puestos en serie. Este resultado era de esperar, pues la interfaz es, en este caso, una equipotencial, por lo que podemos introducir en la misma una placa metálica sin perturbar el sistema y, posteriormente, separar el mismo en dos condensadores con las capacidades indicadas.

@@ Línea 7: / Línea 7: @@
 Para obtener la capacidad de un condensador debemos, o bien fijar la carga sobre una de las placas y, a partir de ella obtener la diferencia de potencial entre placas, o fijar esta última y determinar la carga almacenada.
-Si elegimos este segundo camino, consideramos que la placa inferior (<math>z=0</math>) se encuentra puesta a tierra, mientras que la superior (<math>z=a+b</math>) está a un potencial $V_0$. Para hallar la carga necesitamos el valor de <math>\mathbf{D}</math> y, por tanto, de <math>\mathbf{E}</math>, en el espacio intermedio.
+Si elegimos este segundo camino, consideramos que la placa inferior (<math>z=0</math>) se encuentra puesta a tierra, mientras que la superior (<math>z=a+b</math>) está a un potencial <math>V_0</math>. Para hallar la carga necesitamos el valor de <math>\mathbf{D}</math> y, por tanto, de <math>\mathbf{E}</math>, en el espacio intermedio.
 Al despreciar los efectos de borde, admitimos que el campo es en todo momento perpendicular a las placas, por lo que, en cada región se escribirá
-<center><math>\mathbf{E}=E_i\mathbf{u}_{z}</math>{{qquad}}<math>i=1,2\,</math></center>
+<center><math>\mathbf{E}_i=E_i\mathbf{u}_{z}</math>{{qquad}}<math>i=1,2\,</math></center>
-La condición de que el campo electrostático es irrotacional conduce a
+y, por tratarse de medios lineales
-<center><math>\mathbf{0}=\nabla\times \mathbf{E}=\left|\begin{matrix}\mathbf{u}_{x} & \mathbf{u}_{y} & \mathbf{u}_{z} \\ & & \\
+<center><math>\mathbf{D}_i=\varepsilon_i\mathbf{E}_i=(\varepsilon_iE_i)\mathbf{u}_{z}=D_i\mathbf{u}_z</math>{{qquad}}<math>i=1,2\,</math></center>
-\displaystyle\frac{\partial\ }{\partial x} & \displaystyle\frac{\partial\ }{\partial y} & \displaystyle\frac{\partial\ }{\partial z} \\ & & \\ 0 & 0 & E\end{matrix}\right|=\frac{\partial E}{\partial y}\mathbf{u}_{x}-\frac{\partial E}{\partial x}\mathbf{u}_{y}</math></center>
+esto es, tanto el campo eléctrico como el vector desplzamiento poseen una única componente no nula.
+La condición de que el campo electrostático es irrotacional conduce a que, en cada una de las dos regiones,
+<center><math>\mathbf{0}=\nabla\times \mathbf{E}_i=\left|\begin{matrix}\mathbf{u}_{x} & \mathbf{u}_{y} & \mathbf{u}_{z} \\ & & \\
+\displaystyle\frac{\partial\ }{\partial x} & \displaystyle\frac{\partial\ }{\partial y} & \displaystyle\frac{\partial\ }{\partial z} \\ & & \\ 0 & 0 & E_i\end{matrix}\right|=\frac{\partial E_i}{\partial y}\mathbf{u}_{x}-\frac{\partial E_i}{\partial x}\mathbf{u}_{y}</math></center>
 y, por tanto,
-<center><math>\frac{\partial{}E}{\partial{}x}=\frac{\partial{}E}{\partial{}y}=0</math></center>
+<center><math>\frac{\partial{}E_i}{\partial{}x}=\frac{\partial{}E_i}{\partial{}y}=0</math></center>
 El campo en cada región es independiente de las coordenadas transversales. Sólo dependerá, en todo caso, de la coordenada <math>z</math>.
@@ Línea 26: / Línea 32: @@
 Por su parte, la ley de Gauss en cada medio establece que
-<center><math>\nabla{\cdot}\mathbf{D}=\frac{\partial{}D_z}{\partial{}z}=\rho_l=0</math></center>
+<center><math>\nabla{\cdot}\mathbf{D}_i=\frac{\partial{}D_i}{\partial{}z}=\rho_l=0</math></center>
-por lo que <math>D</math> no depende de <math>z</math>. Por ser  <math>\varepsilon_i</math> uniforme, <math>E</math> tampoco lo hace (compárese este resultado con el del problema de medio estratificado, donde <math>D</math> no depende de <math>z</math>, pero <math>E</math> sí).
+por lo que <math>D_i</math> no depende de <math>z</math>. Por ser  <math>\varepsilon_i</math> uniforme, <math>E_i</math> tampoco lo hace (compárese este resultado con el del problema de medio estratificado, donde <math>\mathbf{D}</math> no depende de <math>z</math>, pero <math>\mathbf{E}</math> sí).
 Por tanto, en cada región, el campo eléctrico es uniforme y va en la dirección <math>z</math>. Sea
@@ Línea 51: / Línea 57: @@
 <center><math>\mathbf{n}{\cdot}[\mathbf{D}]=\mathbf{u}_{z}{\cdot}(\mathbf{D}_2-\mathbf{D}_1)=\varepsilon_2E_2-\varepsilon_1E_1=0</math></center>
-Esta condición se verifica porque suponemos que los dieléctricos son ideales y, por tanto, no hay posibilidad de que la carga libre fluya a través de ellos hasta la interfaz.  Si los dieléctricos no fueran ideal, sino que admitieran el paso de una pequeña corriente, entonces sí podría haber carga libre en la interfaz, como se ve en los [[problemas de corriente eléctrica]].
+Esta condición se verifica porque suponemos que los dieléctricos son ideales y, por tanto, no hay posibilidad de que la carga libre fluya a través de ellos hasta la interfaz.  Si los dieléctricos no fueran ideales, sino que admitieran el paso de una pequeña corriente, entonces sí podría haber carga libre en la interfaz, como se ve en los [[problemas de corriente eléctrica]].
 Así pues, tenemos las dos ecuaciones
@@ Línea 68: / Línea 74: @@
 Conocido <math>\mathbf{D}</math> podemos hallar la carga sobre una de las placas a partir del flujo de este campo a través de una superficie que envuelva la placa.
-Para la placa inferior (la cargada positivamente) el flujo se compone
+Para la placa inferior (la cargada positivamente) el flujo se compone de una parte exterior al condensador (en la cual <math>\mathbf{D}</math> es nulo, ya que se supone que solo hay campos en el interior) y una parte por su interior, en la que la normal va hacia arriba
-de una parte exterior al condensador (en la cual <math>\mathbf{D}</math> es nulo, ya que se supone que solo hay campos en el interior) y una parte por su
-interior, en la que la normal va hacia arriba
 <center><math>Q=\oint\mathbf{D}{\cdot}\mathrm{d}\mathbf{S}=\int_{S_\mathrm{int}}
@@ Línea 82: / Línea 86: @@
 Esta capacidad verifica que
-<center><math>\frac{1}{C}=\frac{\varepsilon_1b+\varepsilon_2a}{\varepsilon_1\varepsilon_2S}=\frac{b}{\varepsilon_2S}+\frac{a}{\varepsilon_1S}
+<center><math>\frac{1}{C}=\frac{\varepsilon_1b+\varepsilon_2a}{\varepsilon_1\varepsilon_2S}=\frac{b}{\varepsilon_2S}+\frac{a}{\varepsilon_1S}=\frac{1}{\displaystyle\frac{\varepsilon_2S}{b}}+\frac{1}{\displaystyle\frac{\varepsilon_1S}{a}}=\frac{1}{C_2}+
-=\frac{1}{\displaystyle\frac{\varepsilon_2S}{b}}+\frac{1}{\displaystyle\frac{\varepsilon_1S}{a}}=\frac{1}{C_2}+
 \frac{1}{C_1}</math></center>
-esto es, equivale a la de dos condensadores puestos en serie. Este resultado era de esperar, pues la interfaz es, en este caso, una equipotencial, por lo que podemos introducir en la misma una placa metálica sin perturbar el sistema y, posteriormente, separar el mismo en dos condensadores con las capacidades indicadas.
+esto es, equivale a la de dos [[condensador plano|condensadores planos]] puestos en serie. Este resultado era de esperar, pues la interfaz es, en este caso, una equipotencial, por lo que podemos introducir en la misma una placa metálica sin perturbar el sistema y, posteriormente, separar el mismo en dos condensadores con las capacidades indicadas.
 [[Categoría:Problemas de materiales dieléctricos]]

Condensador con dos capas de dieléctrico

De Laplace

última version al 19:45 18 feb 2011

1 Enunciado

2 Solución

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES