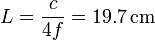Onda estacionaria en un órgano (G.I.A.)
De Laplace
(Diferencias entre revisiones)
(Página creada con '== Enunciado == Determine la longitud de un tubo de órgano cerrado por uno de sus extremos y abierto por el otro, si debe producir una nota de 440 Hz a 25 ºC…') |
(→Solución) |
||
| (Una edición intermedia no se muestra.) | |||
| Línea 7: | Línea 7: | ||
== Solución == | == Solución == | ||
| + | |||
| + | La frecuencia del modo fundamental de vibración en un tubo de órgano es <center><math>f =\dfrac{c}{4L}</math></center> | ||
| + | siendo <math>c</math> la velocidad del sonido en el aire y <math>L</math> la longitud del tubo. | ||
| + | |||
| + | A la temperatura dada en el enunciado la velocidad es | ||
| + | <center><math>c = 331\,\mathrm{\dfrac{m}{s}} + 0.600\mathrm{\dfrac{m}{s\cdot^oC}}25\,\mathrm{^oC}=343\,\mathrm{m/s}</math></center> | ||
| + | |||
| + | |||
| + | Por tanto, la longitud del tubo debe ser | ||
| + | <center><math>L=\dfrac{c}{4f} = 19.7\,\mathrm{cm}</math></center> | ||
| + | |||
| + | [[Categoría:Problemas de movimiento ondulatorio]] | ||
última version al 11:40 13 ene 2011
1 Enunciado
Determine la longitud de un tubo de órgano cerrado por uno de sus extremos y abierto por el otro, si debe producir una nota de 440 Hz a 25 ºC. Admita que la velocidad del sonido en el aire a temperaturas próximas a la ambiente depende de la temperatura como
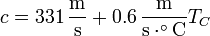
con TC la temperatura en grados centígrados.
2 Solución
La frecuencia del modo fundamental de vibración en un tubo de órgano es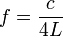
siendo c la velocidad del sonido en el aire y L la longitud del tubo.
A la temperatura dada en el enunciado la velocidad es
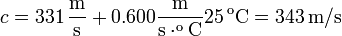
Por tanto, la longitud del tubo debe ser