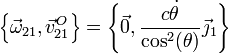6.7. Movimiento de dos varillas articuladas
De Laplace
(→Enunciado) |
|||
| Línea 1: | Línea 1: | ||
==Enunciado== | ==Enunciado== | ||
| - | El mecanismo de la figura está constituido por dos varillas rígidas (sólidos “2” y “0”), de grosor despreciable y longitud indefinida, que se mueven en el plano fijo <math>OX_1Y_1</math> (sólido “1”). La varilla “2” se desplaza verticalmente hacia arriba con velocidad constante <math>v</math>, manteniéndose siempre paralela al eje <math>OY_{\! 1}</math> y a una distancia <math> | + | El mecanismo de la figura está constituido por dos varillas rígidas (sólidos “2” y “0”), de grosor despreciable y longitud indefinida, que se mueven en el plano fijo <math>OX_1Y_1</math> (sólido “1”). La varilla “2” se desplaza verticalmente hacia arriba con velocidad constante <math>v</math>, manteniéndose siempre paralela al eje <math>OY_{\! 1}</math> y a una distancia <math>c</math> de éste; mientras que la varilla “0”, articulada a la anterior en su extremo común A, desliza por el interior de un pasador giratorio ubicado en el punto O del sólido “1”. Utilizando el ángulo <math>\theta</math> (definido en la figura) como parámetro descriptivo del movimiento, se pide: |
# Reducción cinemática de los movimientos {21}, {20} y {01} en el punto O, es decir: <math>\{\vec{\omega}_{\!21};\;\vec{v}^{\,O}_{21}\}</math>, <math>\{\vec{\omega}_{20};\;\vec{v}^{\,O}_{20}\}</math> y <math>\{\vec{\omega}_{01};\;\vec{v}^{\,O}_{01}\}</math>. | # Reducción cinemática de los movimientos {21}, {20} y {01} en el punto O, es decir: <math>\{\vec{\omega}_{\!21};\;\vec{v}^{\,O}_{21}\}</math>, <math>\{\vec{\omega}_{20};\;\vec{v}^{\,O}_{20}\}</math> y <math>\{\vec{\omega}_{01};\;\vec{v}^{\,O}_{01}\}</math>. | ||
| Línea 11: | Línea 11: | ||
==Reducciones cinemáticas== | ==Reducciones cinemáticas== | ||
| - | ===Movimiento {21}== | + | ===Movimiento {21}=== |
La varilla “2” realiza una traslación respecto al sólido “1”, por tanto | La varilla “2” realiza una traslación respecto al sólido “1”, por tanto | ||
| Línea 23: | Línea 23: | ||
<center><math>\vec{v}^A_{21}=\left.\frac{\mathrm{d}\ }{\mathrm{d}t}\overrightarrow{OA}\right|_1 = \frac{c\dot{\theta}}{\cos^2(\theta)}\vec{\jmath}_1</math></center> | <center><math>\vec{v}^A_{21}=\left.\frac{\mathrm{d}\ }{\mathrm{d}t}\overrightarrow{OA}\right|_1 = \frac{c\dot{\theta}}{\cos^2(\theta)}\vec{\jmath}_1</math></center> | ||
| + | |||
| + | En el punto O la reducción es idéntica a la del punto A, por tratarse de una traslación. Por tanto | ||
| + | |||
| + | <center><math>\left\{\vec{\omega}_{21},\vec{v}^O_{21}\right\}=\left\{\vec{0},\frac{c\dot{\theta}}{\cos^2(\theta)}\vec{\jmath}_1\right\}</math></center> | ||
==Posición del CIR== | ==Posición del CIR== | ||
==Aceleraciones== | ==Aceleraciones== | ||
[[Categoría:Problemas de movimiento plano (G.I.T.I.)]] | [[Categoría:Problemas de movimiento plano (G.I.T.I.)]] | ||
Revisión de 21:29 8 ene 2011
Contenido |
1 Enunciado
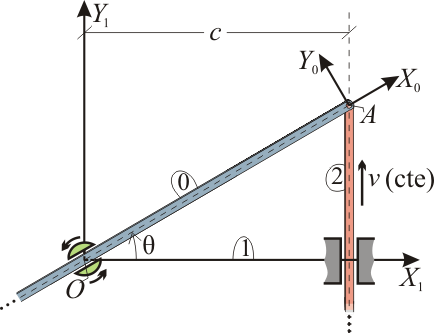
El mecanismo de la figura está constituido por dos varillas rígidas (sólidos “2” y “0”), de grosor despreciable y longitud indefinida, que se mueven en el plano fijo OX1Y1 (sólido “1”). La varilla “2” se desplaza verticalmente hacia arriba con velocidad constante v, manteniéndose siempre paralela al eje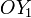 
y a una distancia c de éste; mientras que la varilla “0”, articulada a la anterior en su extremo común A, desliza por el interior de un pasador giratorio ubicado en el punto O del sólido “1”. Utilizando el ángulo θ (definido en la figura) como parámetro descriptivo del movimiento, se pide:
- Reducción cinemática de los movimientos {21}, {20} y {01} en el punto O, es decir:
, 
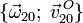y 
.
- Determinación gráfica y determinación analítica de la posición del punto I01, centro instantáneo de rotación del movimiento {01}.
- Cálculo de las aceleraciones
y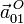 
.
Nota: Para resolver el ejercicio, se propone el uso de la base vectorial asociada al sistema de ejes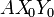 
de la figura, que se mueve solidariamente con la varilla “0” y cuyo eje AX0 es colineal con ella.
2 Reducciones cinemáticas
2.1 Movimiento {21}
La varilla “2” realiza una traslación respecto al sólido “1”, por tanto
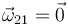
La velocidad de esta traslación la podemos obtener derivando la posición de uno de los puntos del sólido “2”. El punto A, extremo de la barra, tine un vector de posición instantáneo
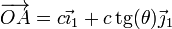
Derivando en esta expresión
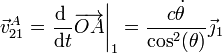
En el punto O la reducción es idéntica a la del punto A, por tratarse de una traslación. Por tanto
