6.7. Movimiento de dos varillas articuladas
De Laplace
(Página creada con '==Enunciado== El mecanismo de la figura está constituido por dos varillas rígidas (sólidos “2” y “0”), de grosor despreciable y longitud indefinida, q…') |
|||
| Línea 1: | Línea 1: | ||
==Enunciado== | ==Enunciado== | ||
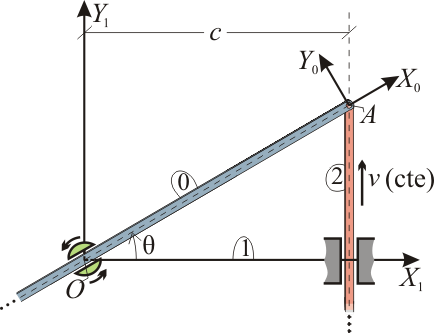
| - | El mecanismo de la figura está constituido por dos varillas rígidas (sólidos “2” y “0”), de grosor despreciable y longitud indefinida, que se mueven en el plano fijo <math>OX_1Y_1</math> (sólido “1”). La varilla “2” se desplaza verticalmente hacia arriba con velocidad constante <math>v</math>, manteniéndose siempre paralela al eje <math>OY_{\! 1}</math> y a una distancia <math>d</math> de éste; mientras que la varilla “0”, articulada a la anterior en su extremo común | + | El mecanismo de la figura está constituido por dos varillas rígidas (sólidos “2” y “0”), de grosor despreciable y longitud indefinida, que se mueven en el plano fijo <math>OX_1Y_1</math> (sólido “1”). La varilla “2” se desplaza verticalmente hacia arriba con velocidad constante <math>v</math>, manteniéndose siempre paralela al eje <math>OY_{\! 1}</math> y a una distancia <math>d</math> de éste; mientras que la varilla “0”, articulada a la anterior en su extremo común A, desliza por el interior de un pasador giratorio ubicado en el punto $O$ del sólido “1”. Utilizando el ángulo <math>\theta</math> (definido en la figura) como parámetro descriptivo del movimiento, se pide: |
# Reducción cinemática de los movimientos {21}, {20} y {01} en el punto O, es decir: <math>\{\vec{\omega}_{\!21};\;\vec{v}^{\,O}_{21}\}</math>, <math>\{\vec{\omega}_{20};\;\vec{v}^{\,O}_{20}\}</math> y <math>\{\vec{\omega}_{01};\;\vec{v}^{\,O}_{01}\}</math>. | # Reducción cinemática de los movimientos {21}, {20} y {01} en el punto O, es decir: <math>\{\vec{\omega}_{\!21};\;\vec{v}^{\,O}_{21}\}</math>, <math>\{\vec{\omega}_{20};\;\vec{v}^{\,O}_{20}\}</math> y <math>\{\vec{\omega}_{01};\;\vec{v}^{\,O}_{01}\}</math>. | ||
| Línea 10: | Línea 10: | ||
<center>[[Archivo:Dos-varillas-articuladas.png]]</center> | <center>[[Archivo:Dos-varillas-articuladas.png]]</center> | ||
| + | ==Reducciones cinemáticas== | ||
| + | ==Posición del CIR== | ||
| + | ==Aceleraciones== | ||
[[Categoría:Problemas de movimiento plano (G.I.T.I.)]] | [[Categoría:Problemas de movimiento plano (G.I.T.I.)]] | ||
Revisión de 21:00 8 ene 2011
Contenido |
1 Enunciado
El mecanismo de la figura está constituido por dos varillas rígidas (sólidos “2” y “0”), de grosor despreciable y longitud indefinida, que se mueven en el plano fijo OX1Y1 (sólido “1”). La varilla “2” se desplaza verticalmente hacia arriba con velocidad constante v, manteniéndose siempre paralela al eje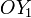 
y a una distancia d de éste; mientras que la varilla “0”, articulada a la anterior en su extremo común A, desliza por el interior de un pasador giratorio ubicado en el punto $O$ del sólido “1”. Utilizando el ángulo θ (definido en la figura) como parámetro descriptivo del movimiento, se pide:
- Reducción cinemática de los movimientos {21}, {20} y {01} en el punto O, es decir:
, 
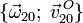y 
.
- Determinación gráfica y determinación analítica de la posición del punto I01, centro instantáneo de rotación del movimiento {01}.
- Cálculo de las aceleraciones
y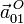 
.
Nota: Para resolver el ejercicio, se propone el uso de la base vectorial asociada al sistema de ejes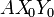 
de la figura, que se mueve solidariamente con la varilla “0” y cuyo eje AX0 es colineal con ella.
