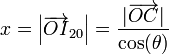6.6. Disco en manivela ranurada
De Laplace
(Página creada con '==Enunciado== El sistema de la figura está constituido por un plano vertical fijo <math>OX_1Y_1</math> (sólido “1”) que en todo instante contiene a otros dos sóli…') |
|||
| Línea 11: | Línea 11: | ||
==Posición del CIR== | ==Posición del CIR== | ||
| + | Por el teorema de los tres centros, el CIR <math>I_{20}</math> debe estar alineado con el <math>I_{21}</math> y el <math>I_{01}</math>. | ||
| + | |||
| + | Por tratarse de una rodadura sin deslizamiento, el CIR del movimiento {21} es el punto de contacto de la rueda con el eje horizontal. | ||
| + | |||
| + | El CIR del movimiento {20} es el punto O, de articulación de la manivela con el eje. | ||
| + | |||
| + | Por estar alineado con estos dos, el CIR del movimiento {20} debe encontrarse sobre el eje horizontal <math>OX_1</math>. Queda por determinar dónde exactamente. | ||
| + | |||
| + | El vínculo de que el centro C del disco se encuentre sobre la manivela obliga a que la velocidad del punto C en el movimiento {20} sea necesariamente a lo largo de ésta. Puesto que el CIR se encuentra sobre la recta que pasa por C y es perpendicular a la velocidad <math>\vec{v}^C_{20}</math> basta con trazar la perpendicular a la manivela en C. El punto donde esta recta corta al eje <math>OX_1</math> es el CIR <math>I_{20}</math>. | ||
| + | |||
| + | El vector de posición de este punto será de la forma | ||
| + | |||
| + | <center><math>\overrightarrow{OI}_{20}=x\vec{\imath}_1</math></center> | ||
| + | |||
| + | El valor de x lo obtenemos aplicando trigonometría. El segmento <math>OI_{20}</math> es la hipotenusa de un triángulo rectángulo cuyo cateto contiguo es <math>OC</math>. Por tanto | ||
| + | |||
| + | <center><math>x = \left|\overrightarrow{OI}_{20}\right| = \frac{|\overrightarrow{OC}|}{\cos(\theta)}</math></center> | ||
| + | |||
| + | |||
==Reducción cinemática== | ==Reducción cinemática== | ||
==Tipo de movimiento== | ==Tipo de movimiento== | ||
[[Categoría:Problemas de movimiento plano (G.I.T.I.)]] | [[Categoría:Problemas de movimiento plano (G.I.T.I.)]] | ||
Revisión de 21:30 2 ene 2011
Contenido |
1 Enunciado
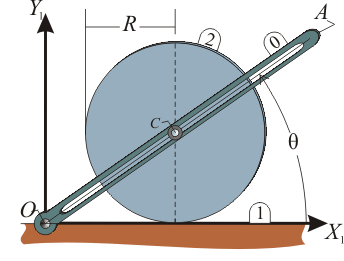
El sistema de la figura está constituido por un plano vertical fijo OX1Y1 (sólido “1”) que en todo instante contiene a otros dos sólidos en movimiento: un disco de radio R y centro C (sólido “2”), que rueda sin deslizar sobre el eje horizontal OX1; y una manivela ranurada OA (sólido “0”), que es obligada a girar con velocidad angular constante Ω alrededor de un eje permanente de rotación que pasa por el punto O y es perpendicular al plano fijo definido como sólido “1” (eje OZ1). Los movimientos de ambos sólidos se hallan vinculados entre sí porque el centro C del disco está obligado a deslizar en todo instante a lo largo de la ranura de la manivela.
Considerando el movimiento {20} como el movimiento problema, se pide:
- Haciendo uso de procedimientos gráficos, determinar la posición del CIR de dicho movimiento {20}.
- Utilizando como parámetro geométrico el ángulo θ indicado en la figura, obtener la reducción cinemática del movimiento {20} en el punto C,
.
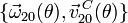- Clasificar el movimiento {20} en el instante en que θ = π / 2 especificando si se trata de rotación, traslación, movimiento helicoidal o reposo.
2 Posición del CIR
Por el teorema de los tres centros, el CIR I20 debe estar alineado con el I21 y el I01.
Por tratarse de una rodadura sin deslizamiento, el CIR del movimiento {21} es el punto de contacto de la rueda con el eje horizontal.
El CIR del movimiento {20} es el punto O, de articulación de la manivela con el eje.
Por estar alineado con estos dos, el CIR del movimiento {20} debe encontrarse sobre el eje horizontal OX1. Queda por determinar dónde exactamente.
El vínculo de que el centro C del disco se encuentre sobre la manivela obliga a que la velocidad del punto C en el movimiento {20} sea necesariamente a lo largo de ésta. Puesto que el CIR se encuentra sobre la recta que pasa por C y es perpendicular a la velocidad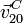 
basta con trazar la perpendicular a la manivela en C. El punto donde esta recta corta al eje OX1 es el CIR I20.
El vector de posición de este punto será de la forma
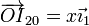
El valor de x lo obtenemos aplicando trigonometría. El segmento OI20 es la hipotenusa de un triángulo rectángulo cuyo cateto contiguo es OC. Por tanto
