Deslizamiento de dos sólidos cónicos
De Laplace
(Página creada con '__TOC__ ==Enunciado== Dos conos rectos “1” y “2” de la misma altura <math>H</math> y mismo radio en la base <math>R</math> se encuentran en contacto a lo…') |
|||
| Línea 1: | Línea 1: | ||
__TOC__ | __TOC__ | ||
==Enunciado== | ==Enunciado== | ||
| - | Dos conos rectos “1” y “2” de la misma altura <math>H</math> y mismo radio en la base <math> | + | Dos conos rectos “1” y “2” de la misma altura <math>H</math> y mismo radio en la base <math>R_0</math> |
se encuentran en contacto a lo largo de una generatriz. Ambos conos se encuentran montados sobre un armazón “0”, de forma que se encuentran rotando con velocidades angulares <math>\vec{\omega}_{10}=\omega_1\vec{k}</math> y <math>\vec{\omega}_{20}=\omega_2\vec{k}</math> alrededor de sus respectivos ejes. Determine la velocidad de deslizamiento en los puntos de contacto de los conos, como función de la altura <math>z</math> medida en la dirección de los ejes desde la base del cono “1”. | se encuentran en contacto a lo largo de una generatriz. Ambos conos se encuentran montados sobre un armazón “0”, de forma que se encuentran rotando con velocidades angulares <math>\vec{\omega}_{10}=\omega_1\vec{k}</math> y <math>\vec{\omega}_{20}=\omega_2\vec{k}</math> alrededor de sus respectivos ejes. Determine la velocidad de deslizamiento en los puntos de contacto de los conos, como función de la altura <math>z</math> medida en la dirección de los ejes desde la base del cono “1”. | ||
| Línea 7: | Línea 7: | ||
==Solución== | ==Solución== | ||
| + | Este es un problema en el que a diferencia del resto, parece la tercera dimensión en el movimiento plano. | ||
| + | |||
| + | En este sistema, tanto en un cono como en el otro, la velocidad de todos los puntos se encuentra contenida en un plano perpendicular al eje OZ y por tanto se trata de un movimiento plano. Sin embargo, la velocidad de deslizamiento depende de la altura porque la sección transversal del movimiento plano depende de por donde hagamos el corte. | ||
| + | |||
| + | Cuando consideramos una sección transversal a una altura <math>z</math>, lo que obtenemos son dos círculos en contacto, cuyos radios dependen de la altura. | ||
| + | |||
| + | El radio del círculo 1 disminuye linealmente con la altura. Para <math>z=0</math> vale <math>R</math> y para <math>z=H</math> vale <math>0</math>. La ecuación de esta recta es | ||
| + | |||
| + | <center><math>R_1(z) = \left(1-\frac{z}{H}\right)R_0</math></center> | ||
| + | |||
| + | El radio del círculo “2” aumenta con <math>z</math> de manera también lineal: | ||
| + | |||
| + | <center><math>R_2(z) = \frac{z}{H}R_0</math></center> | ||
| + | |||
| + | La velocidad de deslizamiento es la velocidad relativa en el punto de contacto, D | ||
| + | |||
| + | <center><math>\vec{v}^D_{21}=\vec{v}^D_{20}-\vec{v}^D_{10}</math></center> | ||
| + | |||
| + | Cada una de estas velocidades corresponde a una rotación respecto a su respectivo eje de rotación, por lo que | ||
| + | |||
| + | <center><math>\vec{v}^D_{21}=\omega_2\vec{k}\times\overrightarrow{I_{20}D}-\omega_1\vec{k}\times\overrightarrow{I_{10}D}</math></center> | ||
| + | |||
| + | Los vectores de posición relativos valen | ||
| + | |||
| + | <center><math>\overrightarrow{I_{20}D}=-R_2\vec{\imath}_0</math>{{qquad}}{{qquad}}<math>\overrightarrow{I_{10}D}=R_1\vec{\imath}_0</math></center> | ||
| + | |||
| + | Llegamos a la velocidad de deslizamiento | ||
| + | |||
| + | <center><math>\vec{v}^D_{20}=-(\omega_1R_1+\omega_2R_2)\vec{\jmath}_0</math></center> | ||
| + | |||
| + | Sustituyendo ahora la dependencia en <math>z</math> | ||
| + | |||
| + | <center><math>\vec{v}^D_{20}=-\left(\omega_1R_0\left(1-\frac{z}{H}\right)+\omega_2R_0\frac{z}{H}\right)\vec{\jmath}_0= | ||
| + | \left(-\omega_1R_0+(\omega_1-\omega_2)R\frac{z}{H}\right)\vec{\jmath}_0</math></center> | ||
| + | |||
| + | Vemos entonces que la velocidad de deslizamiento depende de la altura, pudiendo ser en un sentido, en otro, o nula, según sean las velocidades angulares. | ||
| + | |||
| + | En el caso particular <math>\omega_1=\omega_2</math> no hay dependencia en <math>z</math> y la velocidad de deslizamiento es la misma a todos las alturas. Esto corresponde a que para estas velocidades angulares, uno de los conos se está trasladando respecto al otro. | ||
[[Categoría:Problemas de movimiento plano (G.I.T.I.)]] | [[Categoría:Problemas de movimiento plano (G.I.T.I.)]] | ||
Revisión de 13:36 23 dic 2010
Contenido |
1 Enunciado
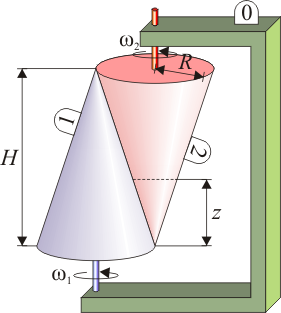
Dos conos rectos “1” y “2” de la misma altura H y mismo radio en la base R0
se encuentran en contacto a lo largo de una generatriz. Ambos conos se encuentran montados sobre un armazón “0”, de forma que se encuentran rotando con velocidades angulares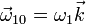 
y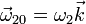 
alrededor de sus respectivos ejes. Determine la velocidad de deslizamiento en los puntos de contacto de los conos, como función de la altura z medida en la dirección de los ejes desde la base del cono “1”.
2 Solución
Este es un problema en el que a diferencia del resto, parece la tercera dimensión en el movimiento plano.
En este sistema, tanto en un cono como en el otro, la velocidad de todos los puntos se encuentra contenida en un plano perpendicular al eje OZ y por tanto se trata de un movimiento plano. Sin embargo, la velocidad de deslizamiento depende de la altura porque la sección transversal del movimiento plano depende de por donde hagamos el corte.
Cuando consideramos una sección transversal a una altura z, lo que obtenemos son dos círculos en contacto, cuyos radios dependen de la altura.
El radio del círculo 1 disminuye linealmente con la altura. Para z = 0 vale R y para z = H vale 0. La ecuación de esta recta es
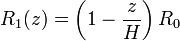
El radio del círculo “2” aumenta con z de manera también lineal:
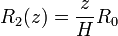
La velocidad de deslizamiento es la velocidad relativa en el punto de contacto, D
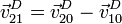
Cada una de estas velocidades corresponde a una rotación respecto a su respectivo eje de rotación, por lo que
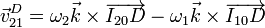
Los vectores de posición relativos valen
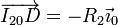
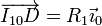
Llegamos a la velocidad de deslizamiento
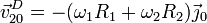
Sustituyendo ahora la dependencia en z
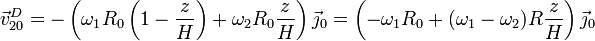
Vemos entonces que la velocidad de deslizamiento depende de la altura, pudiendo ser en un sentido, en otro, o nula, según sean las velocidades angulares.
En el caso particular ω1 = ω2 no hay dependencia en z y la velocidad de deslizamiento es la misma a todos las alturas. Esto corresponde a que para estas velocidades angulares, uno de los conos se está trasladando respecto al otro.
