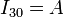6.5. Disco apoyado en placa
De Laplace
(→Enunciado) |
|||
| Línea 11: | Línea 11: | ||
==Centros instantáneos de rotación== | ==Centros instantáneos de rotación== | ||
| + | Tenemos aquí cuatro sólidos y por tanto 6 centros instantáneos de rotación. Algunos de ellos son evidentes, otros requieren el uso del teorema de los tres centros. | ||
| + | |||
| + | ;Movimiento {21}: Dado que el disco rueda sin deslizar sobre la pared vertical, el CIR <math>I_{21}</math> es el punto de contacto B entre el disco y la pared | ||
| + | <center><math>I_{21}=B\,</math></center> | ||
| + | ;Movimiento {20}: El punto C es un un punto material del disco “2” que ocupa una posición fija en el sistema “0” por cómo está definido éste. Al ser nula la velocidad <math>\vec{v}^C_{20}</math>, este punto es el CIR de este movimiento | ||
| + | <center><math>I_{20}=C\,</math></center> | ||
| + | ;Movimiento {30}: Ocurre lo mismo que en el caso anterior, pero con el punto A: es un punto del sólido 3 que ocupa una posición fija en el sistema “0”. Por ello | ||
| + | <center><math>I_{30}=A\,</math></center> | ||
| + | |||
==Reducciones cinemáticas== | ==Reducciones cinemáticas== | ||
[[Categoría:Problemas de movimiento plano (G.I.T.I.)]] | [[Categoría:Problemas de movimiento plano (G.I.T.I.)]] | ||
Revisión de 21:37 21 dic 2010
Contenido |
1 Enunciado
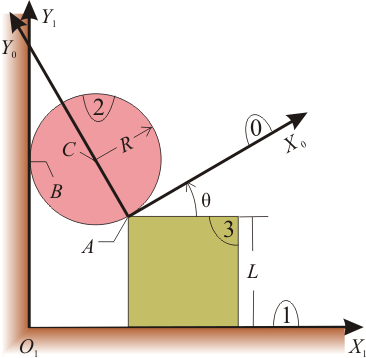
El sistema mecánico de la figura está constituido por los siguientes sólidos rígidos: El plano fijo O1X1Y1 (sólido “1”); la placa cuadrada, de lado L, que desliza sobre el eje O1X1, manteniendo su lado inferior completo en permanente contacto con él (sólido “3”); el disco, de centro en C y radio R, que, en todo instante, rueda sin deslizar sobre el eje O1Y1 en el punto de contacto B, a la vez que rueda y desliza sobre la placa cuadrada en el punto de contacto A (sólido “2”) y el sistema de ejes AX0Y0, definido de tal modo que el eje AY0 contiene permanentemente al centro C del disco, mientras que el eje AX0 es tangente a dicho disco (sólido “0”).
- Para el instante considerado en la figura, determine gráficamente la posición de los centros instantáneos de rotación I21, I20, I03, I23 e I01.
- Utilizando como parámetro el ángulo θ del dibujo (ángulo que forma el eje AX0 con respecto al lado superior de la placa cuadrada), y teniendo presentes las leyes de composición de velocidades y de velocidades angulares aplicadas a {21} = {20} + {03} + {31} halle las siguientes reducciones cinemáticas en C:
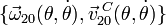 ,
,  ,
,  y
y 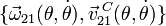 .
.
2 Centros instantáneos de rotación
Tenemos aquí cuatro sólidos y por tanto 6 centros instantáneos de rotación. Algunos de ellos son evidentes, otros requieren el uso del teorema de los tres centros.
- Movimiento {21}
- Dado que el disco rueda sin deslizar sobre la pared vertical, el CIR I21 es el punto de contacto B entre el disco y la pared

- Movimiento {20}
- El punto C es un un punto material del disco “2” que ocupa una posición fija en el sistema “0” por cómo está definido éste. Al ser nula la velocidad
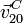 , este punto es el CIR de este movimiento
, este punto es el CIR de este movimiento

- Movimiento {30}
- Ocurre lo mismo que en el caso anterior, pero con el punto A: es un punto del sólido 3 que ocupa una posición fija en el sistema “0”. Por ello