6.2. Movimiento de barra en un pasador
De Laplace
(Diferencias entre revisiones)
(→Enunciado) |
|||
| Línea 1: | Línea 1: | ||
==Enunciado== | ==Enunciado== | ||
| - | La barra <math>AB</math> (sólido “2”), de longitud <math>2a</math>, puede deslizar en su extremo A por el eje <math>OX_1</math> de la escuadra fija <math>OX_1Y_1</math> (sólido “1”), al mismo tiempo que desliza por el interior de un pasador orientable ubicado en el punto C del eje <math>OY_1</math>, a una distancia <math>a</math> del origen O. Sabiendo que la barra gira con velocidad angular constante <math>\ | + | La barra <math>AB</math> (sólido “2”), de longitud <math>2a</math>, puede deslizar en su extremo A por el eje <math>OX_1</math> de la escuadra fija <math>OX_1Y_1</math> (sólido “1”), al mismo tiempo que desliza por el interior de un pasador orientable ubicado en el punto C del eje <math>OY_1</math>, a una distancia <math>a</math> del origen O. Sabiendo que la barra gira con velocidad angular constante <math>\Omega</math> (ley horaria <math>\theta(t)=\Omega t</math>, donde <math>\theta</math> es el ángulo definido en la figura), se pide: |
# Determinar gráficamente la posición del centro instantáneo de rotación (CIR) del movimiento {21}. | # Determinar gráficamente la posición del centro instantáneo de rotación (CIR) del movimiento {21}. | ||
Revisión de 19:38 19 dic 2010
Contenido |
1 Enunciado
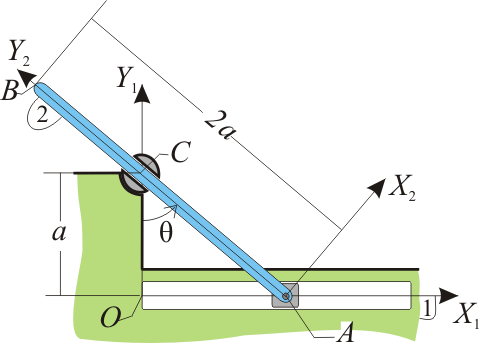
La barra AB (sólido “2”), de longitud 2a, puede deslizar en su extremo A por el eje OX1 de la escuadra fija OX1Y1 (sólido “1”), al mismo tiempo que desliza por el interior de un pasador orientable ubicado en el punto C del eje OY1, a una distancia a del origen O. Sabiendo que la barra gira con velocidad angular constante Ω (ley horaria θ(t) = Ωt, donde θ es el ángulo definido en la figura), se pide:
- Determinar gráficamente la posición del centro instantáneo de rotación (CIR) del movimiento {21}.
- Calcular las velocidades,
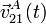y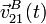 
, y las aceleraciones, 
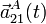y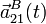 
, de los dos extremos de la barra en cualquier instante de tiempo.
- Determinar analíticamente la posición del C.I.R. del movimiento {21}.
2 Obtención gráfica del CIR
Para hallar la posición del centro instantáneo de rotación existen a menudo varias alternativas posibles.
