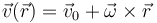Campos equiproyectivos y campo de momentos
De Laplace
(Diferencias entre revisiones)
(→Campo equiproyectivo implica campo de momentos) |
(→Campo equiproyectivo implica campo de momentos) |
||
| Línea 5: | Línea 5: | ||
La condición de equiproyectividad para un campo vectorial <math>\vec{v}(\vec{r})</math> puede expresarse como que para cualesquiera dos puntos <math>\vec{r}_1</math> y <math>\vec{r}_2</math>se verifica | La condición de equiproyectividad para un campo vectorial <math>\vec{v}(\vec{r})</math> puede expresarse como que para cualesquiera dos puntos <math>\vec{r}_1</math> y <math>\vec{r}_2</math>se verifica | ||
| - | <math>\vec{v}(\vec{r}_1)\cdot\left(\vec{r}_2-\vec{r}_1\right)= \vec{v}(\vec{r}_2)\cdot\left(\vec{r}_2-\vec{r}_1\right)</math> | + | <center><math>\vec{v}(\vec{r}_1)\cdot\left(\vec{r}_2-\vec{r}_1\right)= \vec{v}(\vec{r}_2)\cdot\left(\vec{r}_2-\vec{r}_1\right)</math></center> |
se trata de demostrar que si se cumple esta condición, <math>\vec{v}(\vec{r})</math> puede escribirse en la forma | se trata de demostrar que si se cumple esta condición, <math>\vec{v}(\vec{r})</math> puede escribirse en la forma | ||
Revisión de 08:47 18 jun 2008
Contenido |
1 Enunciado del teorema
Un campo vectorial es equiproyectivo sí y solo sí es un campo de momentos de un vector deslizante.
2 Demostración
2.1 Campo equiproyectivo implica campo de momentos
La condición de equiproyectividad para un campo vectorial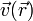 
puede expresarse como que para cualesquiera dos puntos 
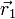y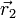 
se verifica
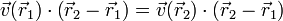
se trata de demostrar que si se cumple esta condición, 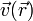puede escribirse en la forma
