Problemas de movimiento plano (G.I.T.I.)
De Laplace
(→Barra apoyada en caja) |
(→Dos rodillos con deslizamiento entre ellos) |
||
| Línea 28: | Línea 28: | ||
==[[Dos rodillos con deslizamiento entre ellos]]== | ==[[Dos rodillos con deslizamiento entre ellos]]== | ||
| - | Un rodillo de radio <math>R=60\,\mathrm{cm}</math> (sólido “0”) rueda sin deslizar sobre un suelo horizontal “1” de forma que su centro C avanza con una celeridad constante <math>v_0=30\,\mathrm{cm}/\mathrm{s}</math> respecto al suelo. En su marcha, este rodillo empuja | + | Un rodillo de radio <math>R=60\,\mathrm{cm}</math> (sólido “0”) rueda sin deslizar sobre un suelo horizontal “1” de forma que su centro C avanza con una celeridad constante <math>v_0=30\,\mathrm{cm}/\mathrm{s}</math> respecto al suelo. En su marcha, este rodillo empuja a un segundo rodillo de radio <math>r=15\,\mathrm{cm}</math> (sólido “2”), que se ve obligado a rodar sin deslizar sobre el mismo suelo, manteniéndose tangente al primer rodillo (ver figura). |
# Calcule las velocidades angulares <math>\vec{\omega}_{21}</math>, <math>\vec{\omega}_{01}</math> y <math>\vec{\omega}_{20}</math>. | # Calcule las velocidades angulares <math>\vec{\omega}_{21}</math>, <math>\vec{\omega}_{01}</math> y <math>\vec{\omega}_{20}</math>. | ||
Revisión de 19:48 9 dic 2010
Contenido |
1 Movimiento de un aro en un pasador
Sea un aro de centro C y radio R (sólido “2”) que se mueve, en un plano fijo OX1Y1 (sólido 1), de tal modo que está obligado a deslizar en todo instante por el interior de un pasador giratorio situado en el punto O, y además se halla articulado en su punto A a un deslizador que se mueve siempre sobre el eje horizontal OX1 (ver figura). Con carácter auxiliar, se define el sistema de ejes AX2Y2 (sólido 2) solidario con el aro en su movimiento.
- Determine gráfica y analíticamente la posición del C.I.R. del movimiento {21}.
- Sabiendo que el ángulo θ, que forman los ejes OX1 y AX2, verifica la ley horaria θ(t) = ωt (donde ω es una constante conocida), calcule
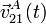y 
.
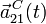2 Movimiento de barra en un pasador
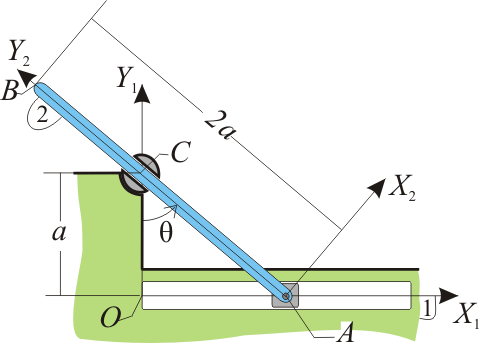
La barra AB (sólido “2”), de longitud 2a, puede deslizar en su extremo A por el eje OX1 de la escuadra fija OX1Y1 (sólido “1”), al mismo tiempo que desliza por el interior de un pasador orientable ubicado en el punto C del eje OY1, a una distancia a del origen O. Sabiendo que la barra gira con velocidad angular constante ω (ley horaria θ(t) = ωt, donde θ es el ángulo definido en la figura), se pide:
- Determinar gráficamente la posición del C.I.R. del movimiento {21}.
- Calcular las velocidades, 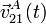y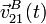
, y las aceleraciones, 
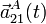y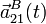 
, de los dos extremos de la barra en cualquier instante de tiempo.
- Determinar analíticamente la posición del C.I.R. del movimiento {21}.
3 Ejemplo paramétrico de movimiento plano
Un sólido “2” se mueve respecto a un sólido “1” de forma que su origen de coordenadas, O2 sigue la ecuación paramétrica
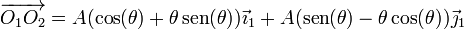
siendo θ = θ(t) el ángulo que el eje O2X2 forma con el O1X1.
- Calcule la velocidad y la aceleración instantáneas del punto O1 en el movimiento {21}:
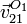y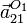 
.
- Determine la posición del CIR I21 respecto al sistema de referencia ligado al sólido “1”.
- Exprese la posición del mismo CIR I21 empleando el sistema de referencia ligado al sólido “2”.
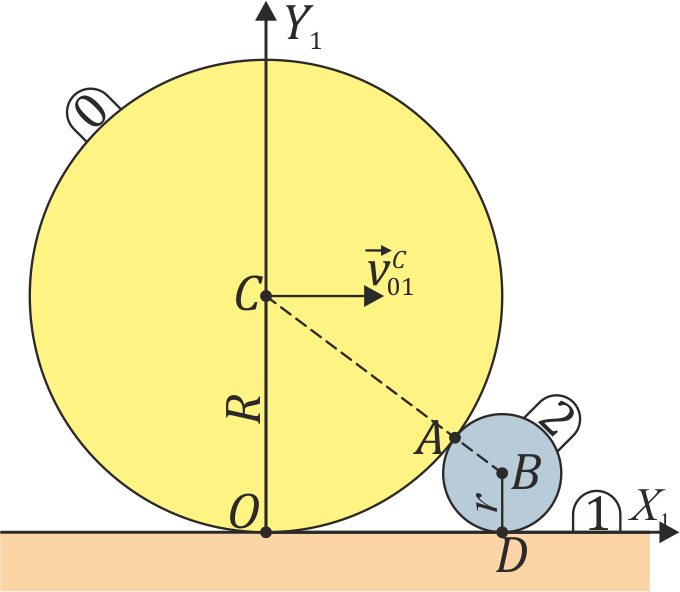
4 Dos rodillos con deslizamiento entre ellos
Un rodillo de radio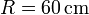 
(sólido “0”) rueda sin deslizar sobre un suelo horizontal “1” de forma que su centro C avanza con una celeridad constante 
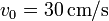respecto al suelo. En su marcha, este rodillo empuja a un segundo rodillo de radio 
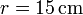(sólido “2”), que se ve obligado a rodar sin deslizar sobre el mismo suelo, manteniéndose tangente al primer rodillo (ver figura).
- Calcule las velocidades angulares
, 
y 
.
- Halle la velocidad relativa de deslizamiento en el punto A de contacto entre los dos sólidos
.
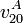- Determine la posición del centro instantáneo de rotación I20.
5 Dos rodillos con deslizamiento con el suelo
Suponga que en la configuración de los dos rodillos del problema anterior de dos rodillos el rozamiento del rodillo “2” con el “0” es mayor que con el suelo, de manera que el rodillo “2” debe rodar sin deslizar sobre el rodillo “0” (y rodar y deslizar sobre el suelo). Halle, para ese caso, la velocidad angular , la de deslizamiento del rodillo “2” sobre el suelo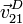 
y la posición del CIR I21.
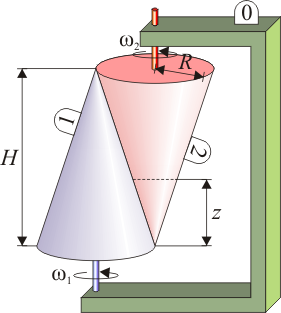
6 Deslizamiento de dos sólidos cónicos
Dos conos rectos “1” y “2” de la misma altura H y mismo radio en la base R
se encuentran en contacto a lo largo de una generatriz. Ambos conos se encuentran montados sobre un armazón “0”, de forma que se encuentran rotando con velocidades angulares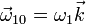 
y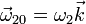 
alrededor de sus respectivos ejes. Determine la velocidad de deslizamiento en los puntos de contacto de los conos, como función de la altura z medida en la dirección de los ejes desde la base del cono “1”.
7 Barra apoyada en caja
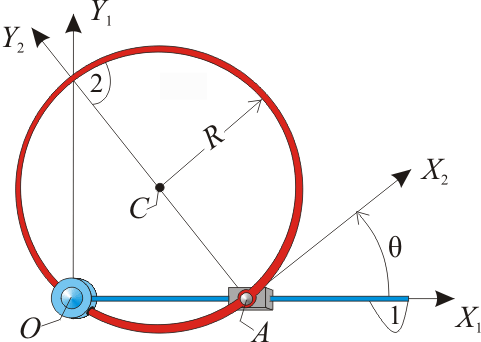
El esquema de la figura muestra una placa cuadrada de lado a (sólido ``0"), uno de cuyos lados desliza sobre el eje horizontal fijo OX1 (sólido “1”), mientras que la placa permanece contenida siempre en el plano vertical fijo OX1Y1. Sobre el vértice $A$ de dicha placa se apoya en todo instante una varilla delgada (sólido “2”), que gira con velocidad angular constante 
, alrededor de su extremo articulado en el punto fijo $O$ (ver figura). Se pide:
- Determinar gráficamente la posición de los centros instantáneos de rotación I21, I02 e I01.
- Calcular: i) La velocidad del vértice A de la placa en el movimiento de ésta respecto de los ejes fijos (movimiento {01}), expresada en función de la posición del sistema:
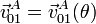. ii) El vector rotación 
, correspondiente al movimiento relativo de la placa respecto de la varilla (movimiento {02}).
- Determinar analíticamente la posición del C.I.R del movimiento {02} (en función del ángulo θ).
