Problemas de movimiento plano (G.I.T.I.)
De Laplace
(Diferencias entre revisiones)
| Línea 1: | Línea 1: | ||
| + | ==[[Movimiento de un aro en un pasador]]== | ||
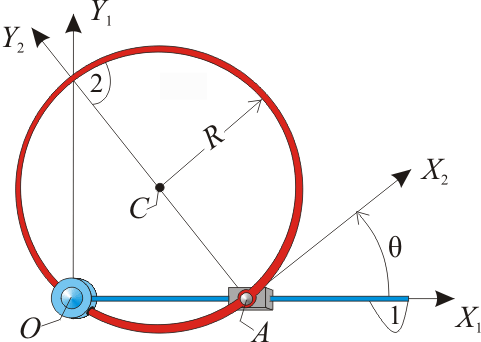
| + | Sea un aro de centro <math>C</math> y radio <math>R</math> (sólido “2”) que se mueve, en un plano fijo <math>OX_1Y_1</math> (sólido <math>1</math>), de tal modo que está obligado a deslizar en todo instante por el interior de un pasador giratorio situado en el punto <math>O</math>, y además se halla articulado en su punto <math>A</math> a un deslizador que se mueve siempre sobre el eje horizontal <math>OX_1</math> (ver figura). Con carácter auxiliar, se define el sistema de ejes <math>AX_2Y_2</math> (sólido <math>2</math>) solidario con el aro en su movimiento. | ||
| + | |||
| + | # Determine gráfica y analíticamente la posición del C.I.R. del movimiento {21}. | ||
| + | # Sabiendo que el ángulo <math>\theta</math>, que forman los ejes <math>OX_1</math> y <math>AX_2</math>, verifica la ley horaria <math>\theta(t)=\omega t</math> (donde <math>\omega</math> es una constante conocida), calcule <math>\vec{v}^{A}_{21}(t)</math> y <math>\vec{a}^{\, C}_{21}(t)</math>. | ||
| + | |||
| + | <center>[[Archivo:aro-pasador.png]]</center> | ||
| + | |||
[[Categoría:Problemas de movimiento plano (G.I.T.I.)|0]] | [[Categoría:Problemas de movimiento plano (G.I.T.I.)|0]] | ||
[[Categoría:Movimiento plano (G.I.T.I.)]] | [[Categoría:Movimiento plano (G.I.T.I.)]] | ||
[[Categoría:Problemas de Física I (G.I.T.I.)|7]] | [[Categoría:Problemas de Física I (G.I.T.I.)|7]] | ||
Revisión de 22:56 8 dic 2010
Movimiento de un aro en un pasador
Sea un aro de centro C y radio R (sólido “2”) que se mueve, en un plano fijo OX1Y1 (sólido 1), de tal modo que está obligado a deslizar en todo instante por el interior de un pasador giratorio situado en el punto O, y además se halla articulado en su punto A a un deslizador que se mueve siempre sobre el eje horizontal OX1 (ver figura). Con carácter auxiliar, se define el sistema de ejes AX2Y2 (sólido 2) solidario con el aro en su movimiento.
- Determine gráfica y analíticamente la posición del C.I.R. del movimiento {21}.
- Sabiendo que el ángulo θ, que forman los ejes OX1 y AX2, verifica la ley horaria θ(t) = ωt (donde ω es una constante conocida), calcule
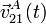 y
y 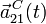 .
.