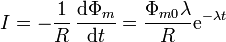Espira cuadrada en torno a solenoide
De Laplace
(→Corriente que circula por la espira) |
(→Corriente que circula por la espira) |
||
| Línea 15: | Línea 15: | ||
==Solución== | ==Solución== | ||
===Corriente que circula por la espira=== | ===Corriente que circula por la espira=== | ||
| - | La corriente que circula por la espira puede obtenerse aplicando la ley de Faraday | + | La corriente que circula por la espira puede obtenerse aplicando la ley de Faraday a una superficie apoyada en la espira |
| - | a una superficie apoyada en la espira | + | |
<center><math>I=\frac{\mathcal{E}}{R}=-\frac{1}{R}\, | <center><math>I=\frac{\mathcal{E}}{R}=-\frac{1}{R}\, | ||
\frac{\mathrm{d}\Phi_m}{\mathrm{d}t}</math></center> | \frac{\mathrm{d}\Phi_m}{\mathrm{d}t}</math></center> | ||
| + | |||
| + | donde consideramos un sentido de recorrido a lo largo del cuadrado tal que la normal a la superficie vaya en el mismo sentido que el campo del solenoide. | ||
Antes de <math>t=0</math> la corriente que circula por la bobina es constante, y lo mismo ocurrirá con su flujo, por lo que no circulará corriente por la espira: | Antes de <math>t=0</math> la corriente que circula por la bobina es constante, y lo mismo ocurrirá con su flujo, por lo que no circulará corriente por la espira: | ||
Revisión de 09:10 17 jun 2008
Contenido |
1 Enunciado
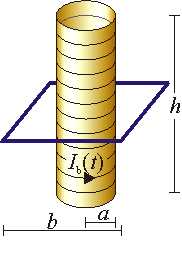
Una espira cuadrada de lado b, de resistencia R y autoinducción despreciable rodea concéntricamente a un solenoide circular largo, de radio a, de longitud h (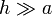 ) y N espiras. Por el solenoide circula una corriente constante Ib0, que a partir de t = 0 comienza a decaer exponencialmente como
) y N espiras. Por el solenoide circula una corriente constante Ib0, que a partir de t = 0 comienza a decaer exponencialmente como
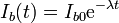
- Sabiendo que el campo magnético en el interior del solenoide es aproximadamente uniforme, calcule la corriente que circula por la espira cuadrada como función del tiempo.
- Halle la carga que pasa por un punto de la espira durante todo el periodo t > 0.
- Halle la potencia instantánea disipada por efecto Joule en la espira, así como la energía total disipada en el periodo t > 0.
- Suponga ahora la misma situación descrita anteriormente, pero considere que la espira posee una autoinducción no despreciable L y que inicialmente no circula corriente por ella. Para t > 0 la corriente que pasa por la espira es de la forma
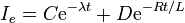
- Calcule las constantes C y D, así como la carga que pasa por un punto de la espira en el periodo t > 0 y la energía total disipada en el mismo periodo.
2 Solución
2.1 Corriente que circula por la espira
La corriente que circula por la espira puede obtenerse aplicando la ley de Faraday a una superficie apoyada en la espira
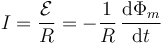
donde consideramos un sentido de recorrido a lo largo del cuadrado tal que la normal a la superficie vaya en el mismo sentido que el campo del solenoide.
Antes de t = 0 la corriente que circula por la bobina es constante, y lo mismo ocurrirá con su flujo, por lo que no circulará corriente por la espira:
A partir de t=0 la corriente del solenoide y el campo que produce dependen del tiempo, por lo que se inducirá una corriente en la espira.
El campo magnético producido por un solenoide circular largo es
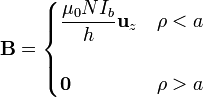
siendo uniforme en el interior del solenoide y nulo fuera.
La dependencia temporal aparece en la corriente Ib, que decae exponencialmente. Por ello, podremos escribir el campo magnético del solenoide como
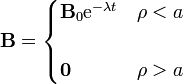
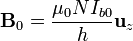
El flujo de este campo a través de un cuadrado apoyado en la espira es
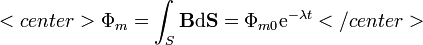
donde
Obsérvese que el área que aparece en el flujo es πa2, la sección del solenoide, y no b2, el área del cuadrado, ya que al ser el campo no nulo únicamente en el interior del solenoide, sólo esta parte contribuye al flujo.
Conocido el flujo, el cálculo de la corriente es inmediato: