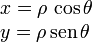Coordenadas polares
De Laplace
(Página creada con '==Definición== right En el caso del movimiento bidimensional de un punto material resulta útil en muchas ocasiones trabajar con '…') |
(→Definición) |
||
| Línea 1: | Línea 1: | ||
==Definición== | ==Definición== | ||
| - | + | ||
En el caso del movimiento bidimensional de un punto material resulta útil en muchas ocasiones trabajar con '''coordenadas polares'''. Usaremos la figura para definirlas. | En el caso del movimiento bidimensional de un punto material resulta útil en muchas ocasiones trabajar con '''coordenadas polares'''. Usaremos la figura para definirlas. | ||
| Línea 29: | Línea 29: | ||
del eje <math>OX </math> aparecerían dos veces, para <math>\theta=0 </math> | del eje <math>OX </math> aparecerían dos veces, para <math>\theta=0 </math> | ||
y para <math>\theta= 2\pi </math>. | y para <math>\theta= 2\pi </math>. | ||
| + | [[Imagen:Coordenadas_polares_definicion.png|right]] | ||
== Relación con las coordenadas cartesianas == | == Relación con las coordenadas cartesianas == | ||
Revisión de 21:40 22 nov 2010
1 Definición
En el caso del movimiento bidimensional de un punto material resulta útil en muchas ocasiones trabajar con coordenadas polares. Usaremos la figura para definirlas.
Sea un punto P situado en el plano OXY con coordenadas cartesianas (x,y). Su vector de posición respecto al origen del sistema de referencia es
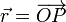
Las coordenadas polares (ρ,θ) se definen de la siguiente forma
- La coordenada ρ es la distancia del punto P al punto O. Puede variar entre los valores 0 y
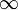 .
.
- La coordenada θ es el ángulo que forma el vector
 con el eje OX. Puede variar entre los valores 0 y 2π.
con el eje OX. Puede variar entre los valores 0 y 2π.
Estas dos coordenadas permiten describir de forma unívoca la posición de cualquier punto en el plano OXY.
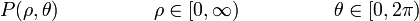
El intervalo para θ es abierto a la derecha para evitar llegar al valor de 2π. De lo contrario, los puntos del eje OX aparecerían dos veces, para θ = 0 y para θ = 2π.
2 Relación con las coordenadas cartesianas
Cada par de valores (x,y) corresponde unívocamente a un par de valores ρ,θ. La relación entre estos dos pares puede obtenerse a partir de la figura.
2.1 Coordenadas cartesianas en función de polares
Teniendo en cuenta las definiciones de seno y coseno trigonométricos, vemos que