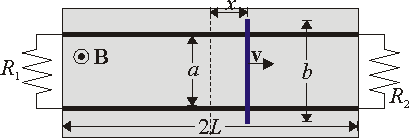
Barra deslizante sobre raíles
De Laplace
(→Corriente en la barra) |
(→Corriente en la barra) |
||
| Línea 33: | Línea 33: | ||
Igualando esta cantidad a la suma de las caídas de tensión a lo largo de la malla, obtenemos la corriente que circula por la malla 1 | Igualando esta cantidad a la suma de las caídas de tensión a lo largo de la malla, obtenemos la corriente que circula por la malla 1 | ||
| - | <center><math>\mathcal{E}_1 = I_1R_1 | + | <center><math>\mathcal{E}_1 = I_1R_1</math>{{qquad}}<math>\Rightarrow</math>{{qquad}}<math>I_1 = -\displaystyle\frac{B_0aV}{R_1}</math></center> |
El signo menos quiere decir que circula en sentido contrario al que hemos elegido como positiva. Esto implica que en la barra la corriente <math>I_1</math> realmente circula hacia abajo, en el sentido del vector <math>-\mathbf{u}_{y}</math>. | El signo menos quiere decir que circula en sentido contrario al que hemos elegido como positiva. Esto implica que en la barra la corriente <math>I_1</math> realmente circula hacia abajo, en el sentido del vector <math>-\mathbf{u}_{y}</math>. | ||
Revisión de 19:23 14 jun 2008
Contenido |
1 Enunciado
Se tienen dos raíles paralelos, perfectamente conductores, de longitud 2L separados una distancia a, tal como se indica en la figura. Los extremos de los raíles están conectados por sendas resistencias R1 y R2. Sobre ellos se desliza una barra también perfectamente conductora de longitud $b$. La barra se desplaza con velocidad constante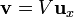 . En el espacio entre los raíles hay aplicado un campo magnético uniforme perpendicular al plano de los raíles,
. En el espacio entre los raíles hay aplicado un campo magnético uniforme perpendicular al plano de los raíles, 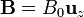 .
.
- Calcule la corriente que circula por la barra.
- Calcule la fuerza ejercida sobre la barra por el campo magnético.
- Halle la potencia disipada por efecto Joule.
2 Solución
2.1 Corriente en la barra
La barra, al ser conductora, tiene cargas libres en su interior. Estas carga se mueven solidariamente con la barra, por tanto con una velocidad perpendicular al campo magnético  . El campo ejerce una fuerza sobre ellas y hace que se mueven a lo largo de la barra. Esto induce una corriente eléctrica. En este caso el circuito tiene dos ramas, una por cada resistencia R1 y R2. En cada rama la intensidad es I1 e I2. En la barra hay que sumar las dos resistencias, pero teniendo cuidado con el signo de cada una de ellas.
. El campo ejerce una fuerza sobre ellas y hace que se mueven a lo largo de la barra. Esto induce una corriente eléctrica. En este caso el circuito tiene dos ramas, una por cada resistencia R1 y R2. En cada rama la intensidad es I1 e I2. En la barra hay que sumar las dos resistencias, pero teniendo cuidado con el signo de cada una de ellas.
En cada rama la fuerza electromotriz inducida se obtiene a partir de la ley de Faraday
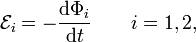
siendo Φ el flujo magnético a través del circuito. En este caso, como hay dos ramas, hay que calcular dos flujos magnéticos. En la figura se indican los dos contornos, con el sentido positivo de circulación. Este sentido proviene de la elección del vector de superficie 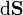 en cada contorno. Lo hemos elegido en la dirección y sentido del eje Z, para que coincida con el campo
en cada contorno. Lo hemos elegido en la dirección y sentido del eje Z, para que coincida con el campo  .
.
El área del contorno izquierdo esta definida por los raíles, la resistencia R1 y la barra. Este área aumenta al desplazarse la barra. Siguiendo la figura, escogemos x = 0 en el centro de los raíles. El área izquierda se puede expresar como
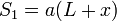
El flujo magnético vale
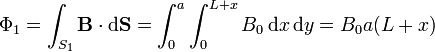
La f.e.m. inducida es

Hemos usado que la posición de la barra es x = Vt.
Igualando esta cantidad a la suma de las caídas de tensión a lo largo de la malla, obtenemos la corriente que circula por la malla 1
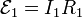

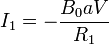
El signo menos quiere decir que circula en sentido contrario al que hemos elegido como positiva. Esto implica que en la barra la corriente I1 realmente circula hacia abajo, en el sentido del vector 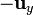 .
.
Para el circuito 2 el procedimiento es similar. El área es

el flujo magnético
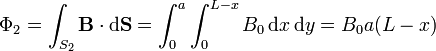
Y la fuerza electromotriz
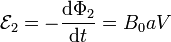
La intensidad I2 sale de
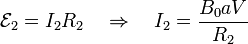
Al ser positiva, el sentido de giro es el indicado en la figura. En la barra la dirección y sentido de I2 coincide con la auténtica de I1, esto es, que aunque hemos asignado sentidos de recorrido opuestos en la barra, realmente las corrientes inducidas suman sus efectos.
La corriente total circulando por la barra hacia abajo es, teniendo en cuenta los sentidos de recorrido asignados
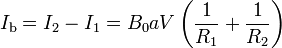
En este sistema, por ser tan simple, no hace falta usar explícitamente las leyes de Kirchhoff. Si la barra tuviera una resistencia Rb, las dos mallas quedarían acopladas y habría que emplear estas leyes para determinar la corriente que circula por cada conductor.
2.2 Fuerza sobre la barra
Para calcular la fuerza usamos la expresión de la ley de Lorentz aplicada a una corriente en un campo externo
En nuestro caso el contorno Γ es la barra central y, al ser el campo uniforme, la fuerza sobre la barra es
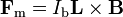
siendo  , indicando la dirección y sentido de la corriente eléctrica en la barra. La fuerza final es
, indicando la dirección y sentido de la corriente eléctrica en la barra. La fuerza final es
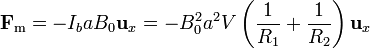
La fuerza se opone al movimiento de la barra. Esto es razonable, pues en caso contrario habríamos descubierto una máquina que produce energía de la nada.
2.3 Balance energético
La barra y los raíles son superconductores, por tanto no disipan energía. Ésta se pierde sólo en las resistencias R1 y R2. Utilizando la expresión de la potencia disipada de la ley de Joule tenemos
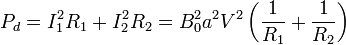
Hemos visto en el apartado anterior que la fuerza magnética sobre la barra se opone a su movimiento, es decir, tiende a frenarla. Para que el movimiento mantenga su velocidad uniforme es necesario ejercer una fuerza sobre la barra que compense a la fuerza magnética. Es el agente que ejerce esta fuerza, ya seamos nosotros con la mano o una máquina externa, quien suministra la energía que se disipa en las resistencias.
Esto puede comprobarse calculando la potencia aportada por este agente externo

Es decir, la potencia externa es la misma que se disipa en las resistencias.