Compresión lineal
De Laplace
(Diferencias entre revisiones)
(→División en dos tramos) |
(→Representación gráfica) |
||
| Línea 13: | Línea 13: | ||
==Representación gráfica== | ==Representación gráfica== | ||
| + | Dado que la presión depende del volumen en la forma | ||
| + | |||
| + | <center><math>p = a + b V\,</math>{{qquad}}{{qquad}}<math>a = 3p_0\,</math>{{qquad}}{{qquad}}<math>b = -\frac{2p_0}{V_0}</math></center> | ||
| + | |||
| + | es claro que la gráfica del proceso es un segmento rectilíneo. El punto inicial del segmento es <math>(p_0,V_0)</math> y el punto final corresponde a <math>V=V_0/2</math> y a la presión | ||
| + | |||
| + | <math>p(V_0/2) = 3p_0 - \frac{2p_0(V_0/2)}{V_0} = 2p_0</math> | ||
| + | |||
| + | Por tanto el volumen final es la mitad del inicial, mientras que la presión es el doble. | ||
| + | |||
==Temperatura final== | ==Temperatura final== | ||
==Trabajo, energía y calor== | ==Trabajo, energía y calor== | ||
Revisión de 16:36 16 nov 2010
Contenido |
1 Enunciado
Se tiene un volumen V0 de un gas ideal diatómico a una presión p0 y una temperatura T0 encerrado en un recipiente con un pistón móvil. Este gas se comprime reversiblemente según la ley
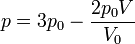
reduciéndose el volumen hasta V0 / 2.
- Trace la gráfica del proceso en un diagrama PV.
- Calcule la temperatura final del proceso.
- Calcule el trabajo neto realizado sobre el gas, la variación de su energía interna y el calor que entra en el gas durante el proceso.
- ¿Para qué volumen durante el proceso la temperatura es máxima? Halle el valor de esta temperatura máxima.
- Separando el proceso en dos: uno hasta que alcanza la temperatura máxima y otro de ahí hasta el final, halle W, ΔU y Q en cada uno de los dos subprocesos.
2 Representación gráfica
Dado que la presión depende del volumen en la forma
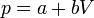
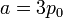

es claro que la gráfica del proceso es un segmento rectilíneo. El punto inicial del segmento es (p0,V0) y el punto final corresponde a V = V0 / 2 y a la presión
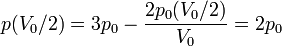
Por tanto el volumen final es la mitad del inicial, mientras que la presión es el doble.





