Entrar Página Discusión Historial Go to the site toolbox

4.6. Identificación de posibles movimientos rígidos

De Laplace

(Diferencias entre revisiones)
Línea 57: Línea 57:
Tenemos las velocidades
Tenemos las velocidades
-
<center><math>2\vec{\imath}+2\vec{\jmath}+4\vec{k}</math>{{qquad}}{{qquad}}<math>2\vec{\imath}+2\vec{\jmath}+4\vec{k}</math>{{qquad}}{{qquad}}<math>2\vec{k}</math></center>
+
<center><math>\vec{v}^A=2\vec{\imath}+2\vec{\jmath}+4\vec{k}</math>{{qquad}}{{qquad}}<math>\vec{v}^B=2\vec{\imath}+2\vec{\jmath}+4\vec{k}</math>{{qquad}}{{qquad}}<math>\vec{v}^C=2\vec{k}</math></center>
Comprobamos primero si se trata de un posible movimiento rígido, chequeando la condición de equiproyectividad para cada par de puntos
Comprobamos primero si se trata de un posible movimiento rígido, chequeando la condición de equiproyectividad para cada par de puntos
Línea 86: Línea 86:
Tenemos las velocidades
Tenemos las velocidades
-
<center><math>2\vec{\imath}+\vec{\jmath}+2\vec{k}</math>{{qquad}}{{qquad}}<math>3\vec{\imath}+2\vec{\jmath}</math>{{qquad}}{{qquad}}<math>2\vec{\imath}+4\vec{\jmath} + 2\vec{k}</math></center>
+
<center><math>\vec{v}^A=2\vec{\imath}+\vec{\jmath}+2\vec{k}</math>{{qquad}}{{qquad}}<math>\vec{v}^B=3\vec{\imath}+2\vec{\jmath}</math>{{qquad}}{{qquad}}<math>\vec{v}^C=2\vec{\imath}+4\vec{\jmath} + 2\vec{k}</math></center>
Comprobamos la equiproyectividad
Comprobamos la equiproyectividad
Línea 113: Línea 113:
Por no se nulo, se trata de un movimiento '''helicoidal'''.
Por no se nulo, se trata de un movimiento '''helicoidal'''.
 +
 +
==Caso III==
 +
El tercer caso
 +
 +
<center><math>\vec{v}^A=2\vec{\imath}+2\vec{\jmath}+2\vec{k}</math>{{qquad}}{{qquad}}<math>\vec{v}^B=2\vec{\imath}+2\vec{\jmath}+2\vec{k}</math>{{qquad}}{{qquad}}<math>\vec{v}^C=2\vec{\imath}+2\vec{\jmath} + 2\vec{k}</math></center>
 +
 +
puede clasificarse por simple inspección. Puesto que las tres velocidades son iguales, y no nulas, se trata de un movimiento de '''traslación'''.
 +
[[Categoría:Problemas de cinemática del sólido rígido (G.I.T.I.)]]
[[Categoría:Problemas de cinemática del sólido rígido (G.I.T.I.)]]

Revisión de 18:17 13 nov 2010

Contenido

1 Enunciado

En un hipotético sólido rígido, consideramos los puntos

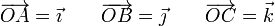
\overrightarrow{OA}=\vec{\imath}\qquad\overrightarrow{OB}=\vec{\jmath}\qquad\overrightarrow{OC}=\vec{k}

y analizamos los casos correspondientes a las siguientes velocidades para los tres puntos:

Caso \vec{v}^A \vec{v}^B \vec{v}^C
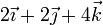
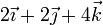
I 2\vec{\imath}+2\vec{\jmath}+4\vec{k} 2\vec{\imath}+2\vec{\jmath}+4\vec{k} 2\vec{k}
II 2\vec{\imath}+\vec{\jmath}+2\vec{k} 3\vec{\imath}+2\vec{\jmath} 2\vec{\imath}+4\vec{\jmath} + 2\vec{k}
III 2\vec{\imath}+2\vec{\jmath}+2\vec{k} 2\vec{\imath}+2\vec{\jmath}+2\vec{k} 2\vec{\imath}+2\vec{\jmath}+2\vec{k}
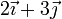
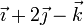
IV 2\vec{\imath}+3\vec{\jmath} \vec{\imath}+2\vec{\jmath}-\vec{k} 4\vec{\imath}+4\vec{\jmath}+2\vec{k}
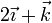
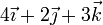
V 2\vec{\imath}+\vec{k} 4\vec{\imath}+2\vec{\jmath}+3\vec{k} 3\vec{\imath}+\vec{\jmath}+2\vec{k}
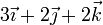
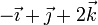
VI 2\vec{\imath}+\vec{\jmath}+2\vec{k} 3\vec{\imath}+2\vec{\jmath}+2\vec{k} -\vec{\imath}+\vec{\jmath}+2\vec{k}

Todas las cantidades están expresadas en las unidades del SI.

Identifique cuáles de las situaciones anteriores son compatibles con la condición de rigidez. Para las que sí lo son, identifique si se trata de un movimiento de traslación pura, rotación pura o helicoidal.

2 Introducción

Para identificar los diferentes estados de movimiento, puesto que lo que se nos da son las velocidades de tres puntos no alineados, es seguir el siguiente esquema:

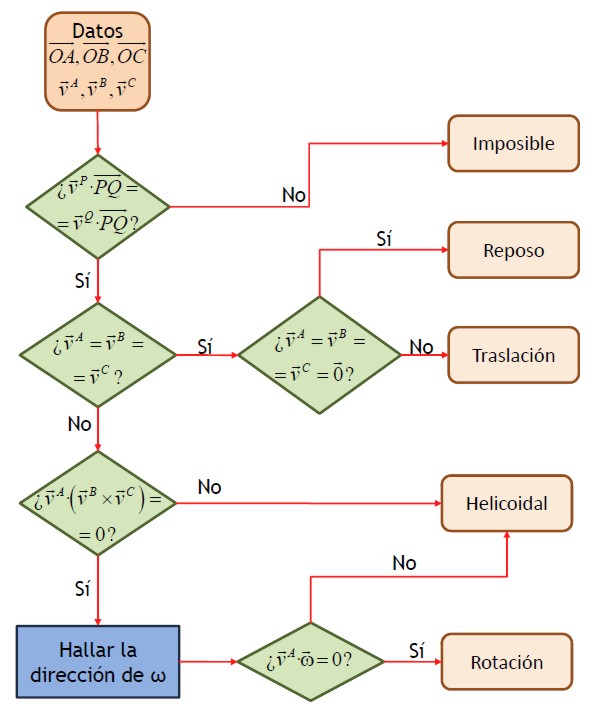
Archivo:flujo-solido-2.jpg

3 Caso I

Tenemos las velocidades

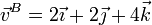
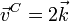
\vec{v}^A=2\vec{\imath}+2\vec{\jmath}+4\vec{k}        \vec{v}^B=2\vec{\imath}+2\vec{\jmath}+4\vec{k}        \vec{v}^C=2\vec{k}

Comprobamos primero si se trata de un posible movimiento rígido, chequeando la condición de equiproyectividad para cada par de puntos

Partículas A y B
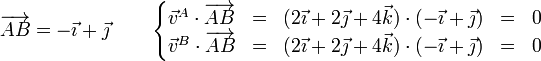
\overrightarrow{AB}=-\vec{\imath}+\vec{\jmath}\qquad\left\{\begin{matrix}\vec{v}^A\cdot\overrightarrow{AB} & = & (2\vec{\imath}+2\vec{\jmath}+4\vec{k})\cdot(-\vec{\imath}+\vec{\jmath}) & = & 0 \\ \vec{v}^B\cdot\overrightarrow{AB} & = & (2\vec{\imath}+2\vec{\jmath}+4\vec{k})\cdot(-\vec{\imath}+\vec{\jmath}) & = & 0 \end{matrix}\right.
Partículas A y C
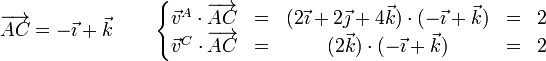
\overrightarrow{AC}=-\vec{\imath}+\vec{k}\qquad\left\{\begin{matrix}\vec{v}^A\cdot\overrightarrow{AC} & = & (2\vec{\imath}+2\vec{\jmath}+4\vec{k})\cdot(-\vec{\imath}+\vec{k}) & = & 2 \\ \vec{v}^C\cdot\overrightarrow{AC} & = & (2\vec{k})\cdot(-\vec{\imath}+\vec{k}) & = & 2 \end{matrix}\right.
Partículas B y C
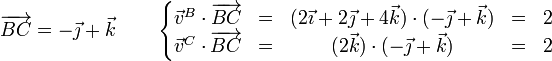
\overrightarrow{BC}=-\vec{\jmath}+\vec{k}\qquad\left\{\begin{matrix}\vec{v}^B\cdot\overrightarrow{BC} & = & (2\vec{\imath}+2\vec{\jmath}+4\vec{k})\cdot(-\vec{\jmath}+\vec{k}) & = & 2 \\ \vec{v}^C\cdot\overrightarrow{BC} & = & (2\vec{k})\cdot(-\vec{\jmath}+\vec{k}) & = & 2 \end{matrix}\right.

Se verifica en los tres casos, por lo que se trata de un movimiento posible para un sólido rígido.

A continuación, comprobamos si las tres velocidades son iguales. No lo son. Por tanto, no puede tratarse de una traslación o un estado de reposo.

Comprobamos ahora si hay dos velocidades iguales. Las hay. Esto quiere decir que el EIRMD es paralelo a la recta que pasa por los dos puntos con la misma velocidad. Para ver si se trata de una rotación, examinamos si cualquiera de las velocidades es perpendicular a esta dirección es perpendicular a esta dirección. No necesitamos volver a calcular nada, ya que lo hicimos previamente:

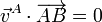
\vec{v}^A\cdot\overrightarrow{AB}=0

Por tanto se trata de un movimiento de rotación pura.

4 Caso II

Tenemos las velocidades

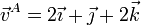
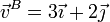
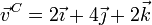
\vec{v}^A=2\vec{\imath}+\vec{\jmath}+2\vec{k}        \vec{v}^B=3\vec{\imath}+2\vec{\jmath}        \vec{v}^C=2\vec{\imath}+4\vec{\jmath} + 2\vec{k}

Comprobamos la equiproyectividad

Partículas A y B
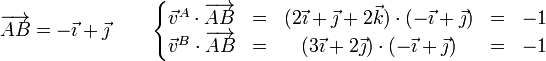
\overrightarrow{AB}=-\vec{\imath}+\vec{\jmath}\qquad\left\{\begin{matrix}\vec{v}^A\cdot\overrightarrow{AB} & = & (2\vec{\imath}+\vec{\jmath}+2\vec{k})\cdot(-\vec{\imath}+\vec{\jmath}) & = & -1 \\ \vec{v}^B\cdot\overrightarrow{AB} & = & (3\vec{\imath}+2\vec{\jmath})\cdot(-\vec{\imath}+\vec{\jmath}) & = & -1 \end{matrix}\right.
Partículas A y C
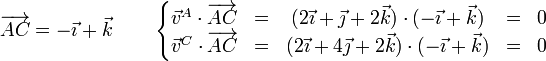
\overrightarrow{AC}=-\vec{\imath}+\vec{k}\qquad\left\{\begin{matrix}\vec{v}^A\cdot\overrightarrow{AC} & = & (2\vec{\imath}+\vec{\jmath}+2\vec{k})\cdot(-\vec{\imath}+\vec{k}) & = & 0 \\ \vec{v}^C\cdot\overrightarrow{AC} & = & (2\vec{\imath}+4\vec{\jmath} + 2\vec{k})\cdot(-\vec{\imath}+\vec{k}) & = & 0 \end{matrix}\right.
Partículas B y C
\overrightarrow{BC}=-\vec{\jmath}+\vec{k}\qquad\left\{\begin{matrix}\vec{v}^B\cdot\overrightarrow{BC} & = & (3\vec{\imath}+2\vec{\jmath})\cdot(-\vec{\jmath}+\vec{k}) & = & -2 \\ \vec{v}^C\cdot\overrightarrow{BC} & = & (2\vec{\imath}+4\vec{\jmath} + 2\vec{k})\cdot(-\vec{\jmath}+\vec{k}) & = & -2 \end{matrix}\right.

De nuevo se verifica en los tres casos, por lo que se trata de un movimiento posible.

Puesto que las tres velocidades no son iguales, no puede tratarse de una traslación o un estado de reposo.

Comprobamos ahora si hay dos velocidades iguales. No las hay.

Verificamos entonces si las velocidades son coplanarias:

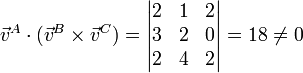
\vec{v}^A\cdot(\vec{v}^B\times\vec{v}^C) = \left|\begin{matrix} 2 & 1 & 2 \\ 3 & 2 & 0 \\ 2 & 4 & 2 \end{matrix}\right| = 18\neq 0

Por no se nulo, se trata de un movimiento helicoidal.

5 Caso III

El tercer caso

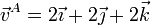
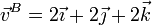
\vec{v}^A=2\vec{\imath}+2\vec{\jmath}+2\vec{k}        \vec{v}^B=2\vec{\imath}+2\vec{\jmath}+2\vec{k}        \vec{v}^C=2\vec{\imath}+2\vec{\jmath} + 2\vec{k}

puede clasificarse por simple inspección. Puesto que las tres velocidades son iguales, y no nulas, se trata de un movimiento de traslación.

Obtenido de "http://tesla.us.es/wiki/index.php/4.6._Identificaci%C3%B3n_de_posibles_movimientos_r%C3%ADgidos"

Herramientas:

Herramientas personales
TOOLBOX
LANGUAGES
licencia de Creative Commons
 Aviso legal - Acerca de Laplace