Diferencia de potencial entre dos discos
De Laplace
(→Pequeña distancia) |
(→Gran distancia) |
||
| (5 ediciones intermedias no se muestran.) | |||
| Línea 36: | Línea 36: | ||
<center><math>\Delta V=\frac{Q a}{\pi\varepsilon_0 R^2}=\frac{1}{4\pi\varepsilon_0} \frac{4 Q a}{R^2}\simeq 9\times 10^9 \frac{4\times 10^{-9}\times 10^{-3}}{10^{-4}}\,\mathrm{V}=360\,\mathrm{V}</math></center> | <center><math>\Delta V=\frac{Q a}{\pi\varepsilon_0 R^2}=\frac{1}{4\pi\varepsilon_0} \frac{4 Q a}{R^2}\simeq 9\times 10^9 \frac{4\times 10^{-9}\times 10^{-3}}{10^{-4}}\,\mathrm{V}=360\,\mathrm{V}</math></center> | ||
| - | Vemos que el voltaje es relativamente elevado, y para una distancia tan pequeña, probablemente se produciría la llamada ruptura | + | Vemos que el voltaje es relativamente elevado, y para una distancia tan pequeña, probablemente se produciría la llamada ''ruptura dieléctrica'', en la que una chispa salta de una placa a la otra, descargando el sistema. |
| - | dieléctrica, en la que una chispa salta de una placa a la otra, descargando el sistema. | + | |
==Gran distancia== | ==Gran distancia== | ||
| + | Si la distancia <math>a=1\,\mathrm{m}</math> no podemos suponer que se trata de dos discos prácticamente infinitos. Por el contrario, cada uno ''ve'' al otro como una carga prácticamente puntual. Al otro, pero no a sí mismo. Para hallar la diferencia de potencial superponemos el efecto de los dos discos, de forma que el potencial en cada punto se escribe | ||
| + | |||
| + | <center><math>\phi(\mathbf{r})=\phi_+(\mathbf{r})+\phi_-(\mathbf{r})</math></center> | ||
| + | |||
| + | Primero tomaremos el de carga positiva, hallaremos el potencial en un punto muy alejado y en su propio centro y calcularemos la diferencia. | ||
| + | Sumando el mismo cálculo para el de carga negativa tendremos la diferencia total. | ||
| + | |||
| + | <center><math>\Delta V = \phi(A)-\phi(B) = | ||
| + | (\phi_+(A)+\phi_-(A))-(\phi_+(B)+\phi_-(B))= (\phi_+(A)-\phi_+(B))+ | ||
| + | (\phi_-(A)-\phi_-(B))=\Delta V_++\Delta V_-\,</math></center> | ||
| + | |||
| + | Para el disco inferior resulta | ||
| + | |||
| + | <center><math>\Delta | ||
| + | V_+=\int_{-a/2}^{a/2}\mathbf{E}_+{\cdot}\mathrm{d}\mathbf{r}=\phi_+(z=-a/2)-\phi_+(z=a/2)</math></center> | ||
| + | |||
| + | En <math>z=-a/2</math> estamos situados en el centro del disco y el potencial en este punto (tomando el origen en el infinito) lo | ||
| + | obtenemos a partir de la expresión | ||
| + | |||
| + | <center><math>\phi_+(\mathbf{r})=\frac{1}{4\pi\varepsilon_0}\int \frac{\sigma_s\,\mathrm{d}S'}{|\mathbf{r}-\mathbf{r}'|}</math></center> | ||
| + | |||
| + | que, en nuestro caso | ||
| + | |||
| + | <center><math>\mathbf{r}=\mathbf{0}</math>{{qquad}}{{qquad}}<math>\mathbf{r}'=\rho'\mathbf{u}_{\rho'}</math>{{qquad}}{{qquad}}<math>|\mathbf{r}-\mathbf{r}'|=\rho'</math>{{qquad}}{{qquad}}<math>\mathrm{d}S'=\rho'\mathrm{d}\rho'\,\mathrm{d}\varphi'</math></center> | ||
| + | |||
| + | |||
| + | <center><math>\phi_+\left(-\frac{a}{2}\right)= | ||
| + | \frac{1}{4\pi\varepsilon_0}\int_0^R\int_0^{2\pi}\frac{\sigma_s\rho'\,\mathrm{d}\varphi'\,\mathrm{d}\rho'}{\rho'}=\frac{\sigma_s R}{2\varepsilon_0}=\frac{Q}{2\pi\varepsilon_0 R}</math></center> | ||
| + | |||
| + | Al desplazarnos al punto <math>z=a/2</math> ya estamos lo suficientemente lejos del disco para verlo como una carga puntual y el potencial en este punto (tomando de nuevo el origen de potencial en el infinito) es, aproximadamente, | ||
| + | |||
| + | <center><math>\phi_+\left(\frac{a}{2}\right)\simeq \frac{Q}{4\pi\varepsilon_0 a}</math></center> | ||
| + | |||
| + | La diferencia de potencial debida al disco de carga positiva vale entonces | ||
| + | |||
| + | <center><math>\Delta V_+\simeq \frac{Q}{2\pi\varepsilon_0 R}-\frac{Q}{4\pi\varepsilon_0 a}</math></center> | ||
| + | |||
| + | Para el disco de carga negativa resulta la misma diferencia de potencial, al cambiar tanto el orden en la resta como el signo de la carga, con lo que | ||
| + | |||
| + | <center><math>\Delta V=\Delta V_++\Delta V_-=\frac{Q}{\pi\varepsilon_0 R}-\frac{Q}{2\pi\varepsilon_0 a}</math></center> | ||
| + | |||
| + | El valor numérico de esta cantidad es | ||
| + | |||
| + | <center><math>\frac{Q}{\pi\varepsilon_0 R}=\frac{1}{4\pi\varepsilon_0}{\cdot}\frac{4Q}{R}\simeq | ||
| + | 3600\,\mathrm{V}</math>{{qquad}}{{qquad}}<math>\frac{2Q}{4\pi\varepsilon_0 a}\simeq 18\,\mathrm{V}</math>{{qquad}}{{qquad}}<math>V=3572\,\mathrm{V}</math></center> | ||
| + | |||
| + | Observemos que, de las dos contribuciones, la primera es mucho más importante y que el resultado es aproximadamente 10 veces el del primer apartado, y no 1000 veces, como podría pensarse ingenuamente al multiplicar la distancia por 1000. | ||
| + | |||
==Distancia arbitraria== | ==Distancia arbitraria== | ||
[[Categoría:Problemas de electrostática en el vacío]] | [[Categoría:Problemas de electrostática en el vacío]] | ||
última version al 10:19 11 nov 2010
Contenido |
1 Enunciado
Se tienen dos discos plásticos de radio 1 cm y espesor despreciable, sobre los cuales se distribuyen de manera uniforme cargas de +1 nC y −1nC respectivamente. Estos discos se disponen paralelamente a una distancia a. Determine
- El valor aproximado de la diferencia de potencial entre los centros cuando la distancia a = 1 mm
- El valor aproximado del voltaje si a = 1 m.
- Determine exactamente la diferencia de potencial entre los centros para cualquier valor de a. Compare el resultado con los dos anteriores. ¿Cuánto es aproximadamente el error cometido en el primer apartado? ¿Y en el segundo?
2 Pequeña distancia
En el primer caso situamos los discos a una distancia mucho menor que su propio radio, siendo uniforme la distribución de carga sobre ellos.
Esta configuración es muy parecida a la de un condensador de placas paralelas, separadas una distancia a, menor que su radio. Como en el caso del condensador, que veremos más adelante, podremos suponer que el campo es uniforme entre los discos.
La aproximación que hacemos consiste en suponer que los discos se comportan como planos de extensión infinita. Esto es razonable siempre que no nos alejemos de ellos tanto que podamos apreciar su tamaño real. El campo creado por dos planos infinitos de carga uniforme, con densidades de carga iguales en magnitud, y opuestas en signo, vale

Para hallar la diferencia de potencial entre centros integramos este campo desde el centro de un disco hasta el del otro. También podemos hallar el potencial en cada punto y calcular la diferencia entre los centros. En este caso no podemos suponer el origen de potencial en el infinito, por tratarse de planos infinitamente extensos. En su lugar, situamos el origen de potencial en el centro del sistema, resultando
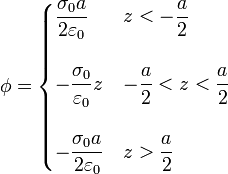
La diferencia de potencial es entonces
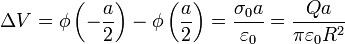
(la densidad de carga, por ser uniforme, equivale a la carga total dividida por la superficie). El valor numérico de esta diferencia es
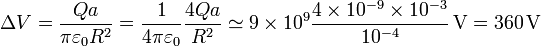
Vemos que el voltaje es relativamente elevado, y para una distancia tan pequeña, probablemente se produciría la llamada ruptura dieléctrica, en la que una chispa salta de una placa a la otra, descargando el sistema.
3 Gran distancia
Si la distancia 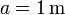 no podemos suponer que se trata de dos discos prácticamente infinitos. Por el contrario, cada uno ve al otro como una carga prácticamente puntual. Al otro, pero no a sí mismo. Para hallar la diferencia de potencial superponemos el efecto de los dos discos, de forma que el potencial en cada punto se escribe
no podemos suponer que se trata de dos discos prácticamente infinitos. Por el contrario, cada uno ve al otro como una carga prácticamente puntual. Al otro, pero no a sí mismo. Para hallar la diferencia de potencial superponemos el efecto de los dos discos, de forma que el potencial en cada punto se escribe
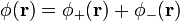
Primero tomaremos el de carga positiva, hallaremos el potencial en un punto muy alejado y en su propio centro y calcularemos la diferencia. Sumando el mismo cálculo para el de carga negativa tendremos la diferencia total.
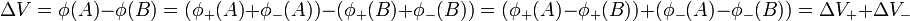
Para el disco inferior resulta
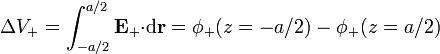
En z = − a / 2 estamos situados en el centro del disco y el potencial en este punto (tomando el origen en el infinito) lo obtenemos a partir de la expresión
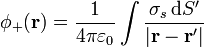
que, en nuestro caso
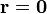
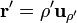

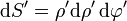
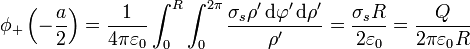
Al desplazarnos al punto z = a / 2 ya estamos lo suficientemente lejos del disco para verlo como una carga puntual y el potencial en este punto (tomando de nuevo el origen de potencial en el infinito) es, aproximadamente,
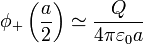
La diferencia de potencial debida al disco de carga positiva vale entonces
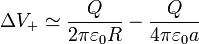
Para el disco de carga negativa resulta la misma diferencia de potencial, al cambiar tanto el orden en la resta como el signo de la carga, con lo que
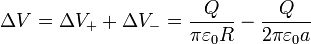
El valor numérico de esta cantidad es
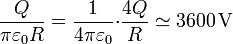
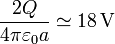

Observemos que, de las dos contribuciones, la primera es mucho más importante y que el resultado es aproximadamente 10 veces el del primer apartado, y no 1000 veces, como podría pensarse ingenuamente al multiplicar la distancia por 1000.





