3.1. Cálculo de energías potenciales
De Laplace
(→Energía potencial) |
(→Gravitación) |
||
| Línea 71: | Línea 71: | ||
(siendo <math>x>0</math>). A diferencia del caso elástico, no podemos tomar el origen de energías potenciales en el centro de fuerzas, <math>\vec{r}=\vec{0}</math>, ya que en ese punto la fuerza tiende a infinito, lo que hace que la integral diverja. En su lugar tomamos como origen de energías potenciales un punto infinitamente alejado del cuerpo atractor, de forma que la integral queda | (siendo <math>x>0</math>). A diferencia del caso elástico, no podemos tomar el origen de energías potenciales en el centro de fuerzas, <math>\vec{r}=\vec{0}</math>, ya que en ese punto la fuerza tiende a infinito, lo que hace que la integral diverja. En su lugar tomamos como origen de energías potenciales un punto infinitamente alejado del cuerpo atractor, de forma que la integral queda | ||
| - | <center><math>U(x) = -\int_{\infty}^x \left(-\frac{GMm}{x^2}\right)\mathrm{d}x = -\left.\frac{GMm}{x}\right | + | <center><math>U(x) = -\int_{\infty}^x \left(-\frac{GMm}{x^2}\right)\mathrm{d}x = -\left.\frac{GMm}{x}\right|_{\infty}^x = -\frac{GMm}{x}</math></center> |
Generalizando para cualquier punto, sea cual sea la orientación respecto a los ejes | Generalizando para cualquier punto, sea cual sea la orientación respecto a los ejes | ||
| Línea 77: | Línea 77: | ||
<center><math>U(\vec{r})=-\frac{GMm}{r}</math></center> | <center><math>U(\vec{r})=-\frac{GMm}{r}</math></center> | ||
| - | Gráficamente, esta función es una hipérbola, que tiende a −& | + | Gráficamente, esta función es una hipérbola, que tiende a −∞ para <math>r\to 0</math>. |
==Curvas de potencial== | ==Curvas de potencial== | ||
Revisión de 20:24 22 oct 2010
Contenido |
1 Enunciado
Para las siguientes fuerzas, consideradas en una dimensión
- Peso: F = − mg
- Elástica: F = − k(x − l0)
- Gravitatoria: F = − GMm / x2
- Determine la energía potencial de la que deriva cada una.
- Trace las curvas de potencial para las tres fuerzas.
- Considere el caso de una partícula sometida simultáneamente a una fuerza elástica y al peso, ¿cuál es la energía potencial como función de la posición? ¿Qué forma tiene su curva de potencial? ¿Qué movimiento describe una partícula sometida a estas dos fuerzas a la vez?
- Para el caso de la fuerza gravitatoria, calcule la velocidad de escape, definida como aquella que partiendo de la superficie de un planeta, permite llegar al infinito con velocidad nula.
2 Energía potencial
Una fuerza se denomina conservativa cuando el trabajo que realiza para ir de un punto a otro
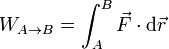
Es independiente del camino que une los dos puntos. En ese caso podemos definir la energía potencial mediante la integral
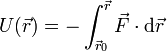
desde un cierto origen de potencial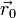 
hasta un punto variable, a lo largo de un camino arbitrario.
En el caso de una fuerza que actúa sobre un solo eje y depende sólo de la posición a lo largo de dicho eje
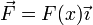
la energía potencial se reduce a la integral escalar
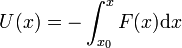
2.1 Peso
En el caso del peso, la fuerza siempre actúa en la dirección vertical, sobre la cual se alinea normalmente el eje OY o el OZ. Considerando que el eje OZ es el vertical y hacia arriba, el peso de una partícula se expresa
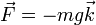
y la energía potencial medida desde una altura z = 0
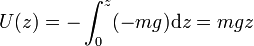
Esta energía aumenta linealmente con la altura. La diferencia de energía potencial entre dos puntos es proporcional a la diferencia de altura entre ellos.
2.2 Resorte
En el caso de un resorte que verifica la ley de Hooke
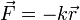
esta fuerza es siempre radial desde el punto de equilibrio del resorte,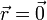 
. Dado un punto del espacio, podemos calcular la energía potencial elástica tomando el eje OX como el que pasa por el punto de equilibrio y el punto en que queramos hallar la energía. En ese caso, sobre este eje, la fuerza se reduce a
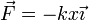
y la energía potencial medida desde la posición central es
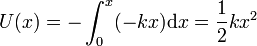
x es aquí la distancia al punto central. Expresando este resultado para cualquier punto del espacio
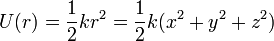
Esta energía crece cuadráticamente con la distancia al centro, siendo su gráfica una parábola.
2.3 Gravitación
Para el caso de la atracción gravitatoria debida a una masa fija, la fuerza estambién radial y dependiente solo de la distancia al centro
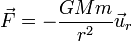
Como en el caso de la ley de Hooke, para cada punto podemos tomar el eje OX como aquél que pasa por el centro de fuerzas y el punto para el cual queremos hallar la energía y escribir la fuerza como
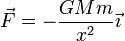
(siendo x > 0). A diferencia del caso elástico, no podemos tomar el origen de energías potenciales en el centro de fuerzas, 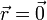, ya que en ese punto la fuerza tiende a infinito, lo que hace que la integral diverja. En su lugar tomamos como origen de energías potenciales un punto infinitamente alejado del cuerpo atractor, de forma que la integral queda
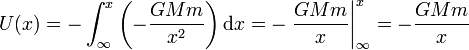
Generalizando para cualquier punto, sea cual sea la orientación respecto a los ejes
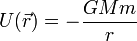
Gráficamente, esta función es una hipérbola, que tiende a −∞ para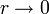 
.
3 Curvas de potencial
3.1 Peso
3.2 Resorte
3.3 Gravitación
4 Resorte con peso
5 Velocidad de escape
La velocidad de escape se define como la mínima velocidad que es preciso comunicar a un cuerpo ligero para salir del campo gravitatorio de otro masivo.
Esta velocidad mínima es la que permite llegar al infinito con velocidad nula. Una velocidad menor no permitiría salir del “pozo” de energía potencial gravitatoria.
La energía mecánica de una partícula en un campo gravitatorio es
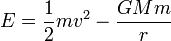
Imponiendo que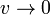 
cuando 
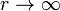queda
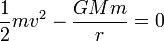
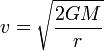
Aquí r es la distancia de partida. En el caso de un cohete que parte de la superficie terrestre r = RT. El valor de GM lo podemos obtener del valor de la aceleración de la gravedad en la superficie terrestre
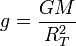
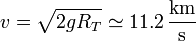
Esta es la velocidad necesaria para salir del campo gravitatorio terrestre. Aparte habrá que comunicarle la velocidad necesaria para enviarlo al destino deseado, teniendo en cuenta la energía potencial gravitatoria debida al Sol.
