Caída a lo largo de una hélice
De Laplace
(→Velocidad) |
|||
| Línea 10: | Línea 10: | ||
En el instante inicial la energía cinética es nula y la energía potencial (tomando como origen el punto más bajo) vale <math>mgb</math>. En el instante final la energía potencial es nula. Por tanto | En el instante inicial la energía cinética es nula y la energía potencial (tomando como origen el punto más bajo) vale <math>mgb</math>. En el instante final la energía potencial es nula. Por tanto | ||
| - | <center><math>0 + mgb = \frac{1}{ | + | <center><math>0 + mgb = \frac{1}{2}mv^2 + 0</math>{{qquad}}{{qquad}}<math>v = \sqrt{2gb}</math></center> |
| - | + | ||
| - | + | ||
| - | + | ||
| + | Esta es la ''rapidez'' con la que se mueve la partícula, pero no su ''velocidad'', que es un vector. La velocidad lleva la dirección del vector tangente | ||
==Fuerza== | ==Fuerza== | ||
[[Categoría:Dinámica del punto material (G.I.T.I.)]] | [[Categoría:Dinámica del punto material (G.I.T.I.)]] | ||
Revisión de 11:04 16 oct 2010
1 Enunciado
Una pequeña anilla de masa m esta obligada a moverse sin rozamiento a lo largo de una hélice de radio A y paso de rosca b cuyo eje está situado verticalmente. La anilla se encuentra sometida a la acción de la gravedad y parte del reposo desde una altura h = b. Cuando se encuentra en z = 0, ¿con qué velocidad se mueve? ¿Qué fuerza ejerce la anilla sobre la hélice?
2 Velocidad
En su movimiento a lo largo de la hélice, la partícula se encuentra sometida a dos fuerzas, la de la gravedad y la fuerza de reacción vincular debida la hélice y que la obliga a moverse a lo largo de ella.
Esta fuerza de reacción vincular es puramente normal a la trayectoria, al no haber rozamiento, y por tanto no realiza trabajo alguno sobre la partícula. Por ello, a la hora de expresar la conservación de la energía mecánica, podemos limitarnos a considerar la acción del peso y escribir
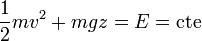
En el instante inicial la energía cinética es nula y la energía potencial (tomando como origen el punto más bajo) vale mgb. En el instante final la energía potencial es nula. Por tanto


Esta es la rapidez con la que se mueve la partícula, pero no su velocidad, que es un vector. La velocidad lleva la dirección del vector tangente





