Problemas de vectores libres (G.I.A.)

De Laplace

Revisión de 15:32 28 sep 2010

1 Suma y diferencia de vectores

1.1 Enunciado

El vector tiene un módulo de 6.00 unidades y forma un ángulo de 36.0 con el eje X, mientras que el vector tiene un módulo de 7.00 unidades y apunta en la dirección negativa del eje X. Calcula la suma y la diferencia de estos dos vectores haciendo uso de los teoremas del seno y del coseno.

1.2 Solución

1.2.1 Teoremas del seno y del coseno

\picskip{0} \parpic[r]{\includegraphics{\camino/triangulo.eps}}

El triángulo de la derecha nos sirve para ilustrar los enunciados del teorema del seno y del teorema del coseno.

\paragraph{Toerema del seno:} dado un triángulo de lados a, b, c, con ángulos 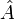, , 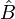, 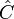indicados en la figura, se cumple \begin{equation}

 \dfrac{a}{\sen \hat{A}}=  \dfrac{b}{\sen \hat{B}}=  \dfrac{c}{\sen \hat{C}}
 \label{teorema_seno}

\end{equation} Vemos que relaciona cada lado con el seno del ángulo opuesto a ese lado.

\paragraph{Teorema del coseno:} dado el triángulo de la figura, la longitud de un lado se expresa como función de las longitudes de los otros dos lados y del ángulo opuesto como \begin{equation}

 \left.
 \begin{array}{l}
   a^2 = b^2 + c^2 - 2bc\cos\hat{A}\\
   b^2 = a^2 + c^2 - 2ac\cos\hat{B}\\
   c^2 = a^2 + b^2 - 2ab\cos\hat{C}
 \end{array}
 \right.
 \label{teorema_coseno}

\end{equation}

1.2.2 Suma de los vectores

\parpic[l]{\includegraphics{\camino/suma.eps}} Vamos a hacer la suma gráficamente. Para ello, podemos colocar un vector detrás de otro y unir el punto de partida con el punto final. Como se observa en la figura, obtenemos un triángulo cuyo tercer lado es el vector No se pudo entender (Falta el ejecutable de <strong>texvc</strong>. Por favor, lea <em>math/README</em> para configurarlo.): \vec{c}=\ab+\vec{b}

que buscamos. De este triangulo conocemos las longitudes de los

lados correspondientes a los vectores No se pudo entender (Falta el ejecutable de <strong>texvc</strong>. Por favor, lea <em>math/README</em> para configurarlo.): \ab

y  y el ángulo δ que forma el vector

No se pudo entender (Falta el ejecutable de <strong>texvc</strong>. Por favor, lea <em>math/README</em> para configurarlo.): \ab

con el eje X. 

Para determinar gráficamente el vector suma necesitamos calcular su módulo (la longitud del lado del triangulo) y el ángulo que forma con el eje X (γ = δ + β).

Usando el teorema del coseno calculamos el módulo del vector 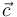\begin{equation}

 c=(a^2+b^2-2\,a\,b\,\cos\delta)^{1/2}
 \label{c_suma}

\end{equation} Una vez conocido c calculamos el ángulo β usando el teorema del seno \begin{equation}

 \dfrac{c}{\sen\delta}=\dfrac{b}{\sen\beta}\Longrightarrow 
 \sen{\beta} = \dfrac{b}{c}\sen\delta
 \label{beta_suma}

\end{equation} Sustituyendo los valores numéricos dados por el enunciado obtenemos \begin{equation}

 \left.
 \begin{array}{l}
   c=(a^2+b^2-2\,a\,b\,\cos\delta)^{1/2}=4.13\\ \\
   \beta = \arcsen\left(\dfrac{b}{c}\sen\delta\right)=85.0^{\circ}=1.48\un{rad}\\ \\
   \gamma=\delta+\beta=121^{\circ}=2.11\un{rad}
 \end{array}
 \right.
 \label{res_suma}

\end{equation} Ahora podemos calcular las componentes cartesianas del vector 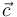\begin{equation}

 \vec{c} = c_x\,\ib + c_y\,\jb = c\,\cos{\gamma}\,\ib + c\,\sen\gamma\,\jb =
 -2.13\,\ib + 3.54\,\jb
 \label{c_suma_cart}

\end{equation} Vemos que el resultado es compatible con el dibujo que hemos utilizado.

1.2.3 Resta de los vectores

\parpic[l]{\includegraphics{\camino/resta.eps}} El procedimiento es similar al caso de la suma. La diferencia es que al final del vector No se pudo entender (Falta el ejecutable de <strong>texvc</strong>. Por favor, lea <em>math/README</em> para configurarlo.): \ab

colocamos

el vector 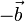, como se indica en la figura. Vemos en el dibujo que el ángulo θ es el suplementario de δ, es decir θ = π − δ (trabajando en radianes). Como en el apartado anterior, usamos el teorema del coseno para calcular el módulo del vector No se pudo entender (Falta el ejecutable de <strong>texvc</strong>. Por favor, lea <em>math/README</em> para configurarlo.): \vec{c}=\ab-\vec{b}

\picskip{0} \begin{equation}

 c=\left( a^2 + b^2 - 2\,a\,b\,\cos\theta \right)^{1/2}=\left( a^2+b^2-2\,a\,b\,\cos(\pi-\delta) \right)^{1/2}=
 \left( a^2+b^2+2\,a\,b\,\cos\delta \right)^{1/2}
 \label{c_resta}

\end{equation} Con el teorema del seno calculamos el ángulo β \begin{equation}

 \dfrac{b}{\sen\beta}=\dfrac{c}{\sen\theta}=\dfrac{c}{\sen(\pi-\delta)}=\dfrac{c}{\sen\delta}
 \Longrightarrow
 \sen\beta=\left( \dfrac{b}{c} \right)\sen\delta
 \label{beta_resta}

\end{equation} El ángulo que forma el vector 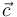con el eje X es γ = δ − β. Sustituyendo los valores numéricos obtenemos \begin{equation}

 \left.
 \begin{array}{l}
   c=\left( a^2+b^2+2\,a\,b\,\cos\delta \right)^{1/2}=12.4\\ \\
   \beta=\arcsin\left( \dfrac{b}{c}\sen\delta \right)=19.4^{\circ}=0.339\un{rad}\\ \\
   \gamma = \delta-\beta = 16.6^\circ=0.290\un{rad}
 \end{array}
 \right.
 \label{res_resta}

\end{equation} Las componentes cartesianas del vector resta son \begin{equation}

 \vec{c} = c_x\,\ib + c_y\,\jb = c\,\cos{\gamma}\,\ib + c\,\sen\gamma\,\jb =
 11.9\,\ib + 3.54\,\jb
 \label{c_resta_cart}

\end{equation}

1.2.4 Resolución usando una base cartesiana

El problema es más fácil de resolver si expresamos los vectores No se pudo entender (Falta el ejecutable de <strong>texvc</strong>. Por favor, lea <em>math/README</em> para configurarlo.): \ab

y  en la base

cartesiana \begin{equation}

 \left.
 \begin{array}{l}
   \ab = a\cos\delta\,\ib+a\sen\delta\,\jb = 4.85\,\ib + 3.53\,\jb\\ \\
   \vec{b}=-7\,\ib
 \end{array}
 \right.

\end{equation} Los vectores suma y resta son \begin{equation}

 \left.
 \begin{array}{l}
   \ab+\vec{b}= -2.15\,\ib + 3.53\,\jb\\ \\
   \ab-\vec{b} = 11.9\,\ib + 3.53\,\jb
 \end{array}
 \right.

\end{equation}