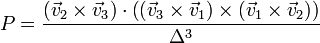Entrar Página Discusión Historial Go to the site toolbox

Cálculo de base dual

De Laplace

(Diferencias entre revisiones)
(Página creada con '==Enunciado== Sea <math>B_1=\{\vec{v}_1,\vec{v}_2,\vec{v}_3\}</math> una base vectorial arbitraria. Sean <math>\{\vec{w}_1,\vec{w}_2,\vec{w}_3\}</math> tres vectores definidos p…')
Línea 27: Línea 27:
: en las bases del apartado anterior.
: en las bases del apartado anterior.
==Carácter de base==
==Carácter de base==
 +
En el espacio de tridimensional ordinario, cualquier conjunto de tres vectores linealmente independientes constituye una base.
 +
 +
Para demostrar la independencia lineal basta probar que el producto mixto de los tres vectores es nulo. Por tanto debemos hallar
 +
 +
<center><math>P = \vec{w}_1\cdot(\vec{w}_2\times\vec{w}_3)</math></center>
 +
 +
Sustituyendo las definiciones de cada uno de los vectores
 +
 +
<center><math>P = \frac{(\vec{v}_2\times\vec{v}_3)\cdot\left((\vec{v}_3\times\vec{v}_1)\times (\vec{v}_1\times\vec{v}_2)\right)}{\Delta^3}</math></center>
==Ortogonalidad==
==Ortogonalidad==
==Componentes de un vector==
==Componentes de un vector==

Revisión de 08:17 26 sep 2010

Contenido

1 Enunciado

Sea 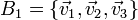B_1=\{\vec{v}_1,\vec{v}_2,\vec{v}_3\} una base vectorial arbitraria. Sean 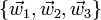\{\vec{w}_1,\vec{w}_2,\vec{w}_3\} tres vectores definidos por

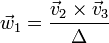
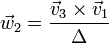
\vec{w}_1=\frac{\vec{v}_2\times\vec{v}_3}{\Delta}        \vec{w}_2=\frac{\vec{v}_3\times\vec{v}_1}{\Delta}        \vec{w}_3=\frac{\vec{v}_1\times\vec{v}_2}{\Delta}        \Delta =\vec{v}_1\cdot(\vec{v}_2\times\vec{v}_3)
1. Demuestre que el conjunto 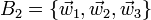B_2=\{\vec{w}_1,\vec{w}_2,\vec{w}_3\} es también una base (llamada base dual de B1). ¿Cuánto vale el producto mixto de sus vectores?
2. Pruebe que se cumple
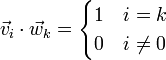
\vec{v}_i\cdot\vec{w}_k=\begin{cases} 1 & i = k \\ 0 & i\neq 0\end{cases}
3. Demuestre que las componentes de un vector en la base B1 pueden calcularse proyectando sobre la base B2, esto es, si
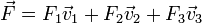
\vec{F} = F_1\vec{v}_1 + F_2\vec{v}_2 + F_3\vec{v}_3
la componente k viene dada por
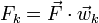
F_k = \vec{F}\cdot\vec{w}_k
4. Halle la base dual de la base
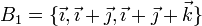
B_1 =\{\vec{\imath},\vec{\imath}+\vec{\jmath},\vec{\imath}+\vec{\jmath}+\vec{k}\}
5. Calcule las componentes del vector
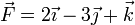
\vec{F} = 2\vec{\imath}-3\vec{\jmath}+\vec{k}
en las bases del apartado anterior.

2 Carácter de base

En el espacio de tridimensional ordinario, cualquier conjunto de tres vectores linealmente independientes constituye una base.

Para demostrar la independencia lineal basta probar que el producto mixto de los tres vectores es nulo. Por tanto debemos hallar

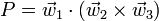
P = \vec{w}_1\cdot(\vec{w}_2\times\vec{w}_3)

Sustituyendo las definiciones de cada uno de los vectores

P = \frac{(\vec{v}_2\times\vec{v}_3)\cdot\left((\vec{v}_3\times\vec{v}_1)\times (\vec{v}_1\times\vec{v}_2)\right)}{\Delta^3}

3 Ortogonalidad

4 Componentes de un vector

5 Caso particular

6 Ejemplo de cálculo de componentes

Obtenido de "http://tesla.us.es/wiki/index.php/C%C3%A1lculo_de_base_dual"

Herramientas:

Herramientas personales
TOOLBOX
LANGUAGES
licencia de Creative Commons
 Aviso legal - Acerca de Laplace