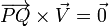1.8. Ejemplo de clasificación de vectores
De Laplace
(Página creada con '==Enunciado== De los siguientes vectores ligados con sus respectivos puntos de aplicación: :a) <math>\vec{v}_1 = 2\vec{\imath}-\vec{\jmath} + \vec{k}</math> en <math>A(3,1,1)\…') |
|||
| Línea 10: | Línea 10: | ||
indique cuáles pueden representar al mismo vector deslizante y cuáles al mismo vector libre. | indique cuáles pueden representar al mismo vector deslizante y cuáles al mismo vector libre. | ||
| + | ==Vectores libres== | ||
| + | La condición para que dos vectores ligados representen al mismo vector libre es que tengan el mismo módulo, dirección y sentido. Equivalentemente, los dos vectores ligados deben ser iguales componente a componente. | ||
| + | |||
| + | Examinando los cinco vectores ligados propuestos, es claro que pueden representar a dos vectores libres: | ||
| + | |||
| + | ;Primer vector:Los vectores ligados <math>\vec{v}_1</math>, <math>\vec{v}_3</math> y <math>\vec{v}_4</math> representan al mismo vector libre | ||
| + | |||
| + | <center><math>\vec{V}_1 = 2\vec{\imath}-\vec{\jmath} + \vec{k}</math></center> | ||
| + | |||
| + | ;Segundo vector:Los vectores ligados <math>\vec{v}_2</math> y <math>\vec{v}_5</math> representan al vector libre | ||
| + | |||
| + | <center><math>\vec{V}_2 = 2\vec{\imath}+\vec{\jmath} + \vec{k}</math></center> | ||
| + | |||
| + | ==Vectores deslizantes== | ||
| + | Para que dos vectores ligados representen al mismo vector deslizante deben coincidir en módulo, dirección y sentido y además sus puntos de aplicación deben encontrarse sobre la misma recta soporte. | ||
| + | |||
| + | Para imponer esta restricción debemos exigir que el vector que une los dos puntos de aplicación sea paralelo al vector deslizante, lo cual se consigue con el producto vectorial | ||
| + | |||
| + | <center><math>\overrightarrow{PQ}\times\vec{V}=\vec{0}</math></center> | ||
[[Categoría:Problemas de vectores libres (G.I.T.I.)]] | [[Categoría:Problemas de vectores libres (G.I.T.I.)]] | ||
Revisión de 13:22 24 sep 2010
1 Enunciado
De los siguientes vectores ligados con sus respectivos puntos de aplicación:
- a)
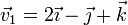 en
en 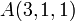
- b)
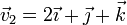 en
en 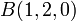
- c)
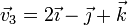 en
en 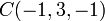
- d)
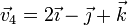 en
en 
- e)
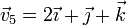 en
en 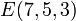
indique cuáles pueden representar al mismo vector deslizante y cuáles al mismo vector libre.
2 Vectores libres
La condición para que dos vectores ligados representen al mismo vector libre es que tengan el mismo módulo, dirección y sentido. Equivalentemente, los dos vectores ligados deben ser iguales componente a componente.
Examinando los cinco vectores ligados propuestos, es claro que pueden representar a dos vectores libres:
- Primer vector
- Los vectores ligados
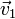 ,
, 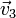 y
y 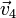 representan al mismo vector libre
representan al mismo vector libre
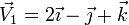
- Segundo vector
- Los vectores ligados
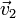 y
y 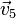 representan al vector libre
representan al vector libre
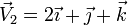
3 Vectores deslizantes
Para que dos vectores ligados representen al mismo vector deslizante deben coincidir en módulo, dirección y sentido y además sus puntos de aplicación deben encontrarse sobre la misma recta soporte.
Para imponer esta restricción debemos exigir que el vector que une los dos puntos de aplicación sea paralelo al vector deslizante, lo cual se consigue con el producto vectorial