2.1. Fórmulas potencialmente incorrectas
De Laplace
| Línea 48: | Línea 48: | ||
Estas dimensiones no son coincidentes (en la segunda falta la masa), por lo que la ecuación es incorrecta. | Estas dimensiones no son coincidentes (en la segunda falta la masa), por lo que la ecuación es incorrecta. | ||
| + | |||
| + | ==Caso (d)== | ||
| + | En la identidad | ||
| + | |||
| + | <math>(\vec{r}\times\vec{p})\vec{L} = R(\vec{r}\cdot\vec{p})\vec{p}</math> | ||
| + | |||
| + | ¿qué tipo de operación aparece en el primer miembro? Tenemos un vector <math>(\vec{r}\times\vec{p})</math> seguido de otro sin ningún signo de producto entre ellos. No es un producto escalar, que lleva un punto, ni uno vectorial (que lleva una cruz o una cuña). Por tanto, el primer miembro carece de significado. No es ni un escalar ni un vector. | ||
| + | |||
| + | Parecería que en el segundo miembro se da el mismo caso, ya que no hay punto o cruz entre <math>(\vec{r}\cdot\vec{p})</math> y <math>\vec{p}</math>, pero no es así, porque el producto escalar es un número, no un vector, y el producto de un escalar por un vector no lleva punto, siendo el resultado un vector. | ||
Revisión de 15:22 23 sep 2010
Contenido |
1 Enunciado
De las siguientes expresiones, indique cuáles son necesariamente incorrectas. Aquí las diferentes letras representan las magnitudes definidas en el problema de ejemplos de análisis dimensional, R es una distancia y  el vector de posición; t es el tiempo:
el vector de posición; t es el tiempo:
- (a)
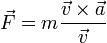
- (b)
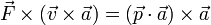
- (c)
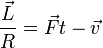
- (d)
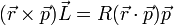
- (e)
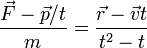
- (f)
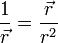
- (g)
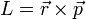
- (h)
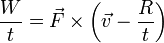
2 Caso (a)
La ecuación
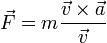
es obviamente incorrecta ya que no está definida la división por un vector. Por tanto, el segundo miembro es absurdo.
3 Caso (b)
En el caso de la expresión
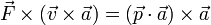
el primer miembro posee significado. Sin embargo, en el segundo miembro encontramos el producto vectorial de 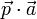 por
por  , pero
, pero 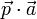 es una cantidad escalar, no vectorial y por tanto no puede multiplicarse vectorialmente por nada. La expresión es incorrecta.
es una cantidad escalar, no vectorial y por tanto no puede multiplicarse vectorialmente por nada. La expresión es incorrecta.
4 Caso (c)
Para la fórmula
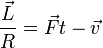
tenemos que el primer miembro es un vector y en el segundo miembro tenemos la diferencia de dos vectores, que es una expresión admisible. Por tanto, esta expresión no es incorrecta, desde el punto de vista vectorial.
No basta, no obstante, con esto. Debemos comprobar que también es dimensionalmente correcta. El primer miembro tiene dimensiones
![\left[\frac{\vec{L}}{R}\right] = \frac{ML^2T^{-1}}{L} = MLT^{-1}](/wiki/images/math/0/9/9/099cddc1a42caa65853c53a7cf9c96e1.png)
En el segundo miembro tenemos
![\left[\vec{F}t\right] = (MLT^{-2})T = MLT^{-1}](/wiki/images/math/5/4/d/54db25bc6873e0a8855fbc4863041dca.png)
![\left[\vec{v}\right]=LT^{-1}](/wiki/images/math/c/c/e/cce06e1e85bb009acd26fc2cf2d6bbf2.png)
Estas dimensiones no son coincidentes (en la segunda falta la masa), por lo que la ecuación es incorrecta.
5 Caso (d)
En la identidad
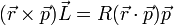
¿qué tipo de operación aparece en el primer miembro? Tenemos un vector 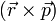 seguido de otro sin ningún signo de producto entre ellos. No es un producto escalar, que lleva un punto, ni uno vectorial (que lleva una cruz o una cuña). Por tanto, el primer miembro carece de significado. No es ni un escalar ni un vector.
seguido de otro sin ningún signo de producto entre ellos. No es un producto escalar, que lleva un punto, ni uno vectorial (que lleva una cruz o una cuña). Por tanto, el primer miembro carece de significado. No es ni un escalar ni un vector.
Parecería que en el segundo miembro se da el mismo caso, ya que no hay punto o cruz entre 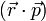 y
y 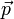 , pero no es así, porque el producto escalar es un número, no un vector, y el producto de un escalar por un vector no lleva punto, siendo el resultado un vector.
, pero no es así, porque el producto escalar es un número, no un vector, y el producto de un escalar por un vector no lleva punto, siendo el resultado un vector.





