Dos discos y barra rodando sin deslizar
De Laplace
(→Aplicación del Teorema de los tres centros) |
(→Aplicación del Teorema de los tres centros) |
||
| Línea 26: | Línea 26: | ||
<center><math>\left.\begin{array}{l}I_{20}\in\Delta(E,F)\\ \\ | <center><math>\left.\begin{array}{l}I_{20}\in\Delta(E,F)\\ \\ | ||
| - | I_{20}\in\Delta( | + | I_{20}\in\Delta(A,B)\end{array}\right\}\quad</math>{{tose}}{{qquad}}<math style="border:solid magenta 2px;padding:7px">I_{20}=\Delta(E,F)\bigcap\Delta(A,B)</math></center> |
| - | Anáologamente, el C.I.R. del movimiento <math>\displaystyle \{31\}</math> (punto <math>\displaystyle I_{31}</math>) debe estar alineado con los puntos <math>A</math> y <math>E</math>, al coincidir éstos con los C.I.R. de los movimientos <math>\displaystyle \{30\}</math> y <math>\displaystyle \{01\}</math> (recuérdese que <math>\displaystyle I_{ij}=I_{ji}</math>). | + | Anáologamente, el C.I.R. del movimiento <math>\displaystyle \{31\}</math> (punto <math>\displaystyle I_{31}</math>) debe estar alineado con los puntos <math>A</math> y <math>E</math>, al coincidir éstos con los C.I.R. de los movimientos <math>\displaystyle \{30\}</math> y <math>\displaystyle \{01\}</math> (recuérdese que <math>\displaystyle I_{ij}=I_{ji}</math>). Pero además, dicho punto debe estar en la recta <math>\Delta (A,F)</math>, que pasa por los centros de los movimientos <math>\displaystyle \{32\}</math> y <math>\displaystyle \{21\}</math>. |
| + | |||
| + | <center>[[Archivo:P1_sep_09_19_1.gif]]</center> | ||
==Reducciones cinemáticas== | ==Reducciones cinemáticas== | ||
Revisión de 22:16 20 sep 2010
Contenido |
1 Enunciado
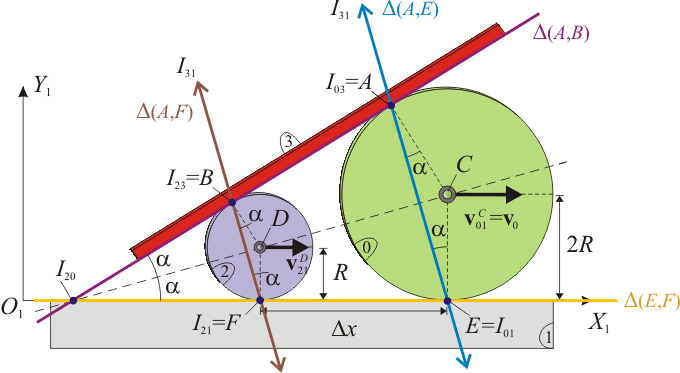
Sendos discos de radios radios 2R y R (sólidos “0” y “2”, respectivamente) se encuentran siempre contenidos en el mismo plano y en contacto puntual sobre el sólido fijo “1”. Además, hay una barra rígida (sólido “3”), también contenida en el plano de los discos y en contacto puntual con éstos. El sistema se mueve de manera que los discos “0” y “2” ruedan sin deslizar de manera simultánea sobre los sólidos “1” y “3”.
- Determine los C.I.R. de los diferentes movimientos relativos en el sistema descrito. ¿Cómo es el movimiento instantáneo de la barra “3” respecto del sólido fijo “1”?
- Suponiendo que en el movimiento del disco de mayor radio respecto del sólido fijo la velocidad de su centro C es un vector constante de valor conocido
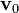, determine las reducciones cinemáticas de los movimientos {01}, {21} y {31}.
- Determine la ley horaria que sigue la distancia
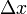entre los puntos de contacto de los discos con el sólido fijo. Supóngase que en el instante inicial esta distancia es 3R.
- Determine la reducción cinemática del movimiento relativo del disco pequeño respecto del grande, {20}. Calcule la aceleración instantánea del centro D en dicho movimiento.
2 C.I.R. de los movimientos
Las posiciones que en un instante dado ocupan los centros instantáneos de rotación (C.I.R.) de los movimientos planos realizados por los discos “0” y “2” respecto del sólido fijo “1” y de la barra “3” se determinan de manera inmediata: en la descripción del movimiento del sistema se indica que los discos siempre ruedan sin deslizar sobre sólido y fijo y barra. Por tanto, las velocidades relativas de los puntos de contacto son nulas y, en consecuencia, éstos coinciden con los C.I.R. correspondientes a dichos movimientos.
Denominemos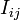 
al C.I.R. del movimiento 
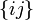; si en un determinado instante A y B son los puntos de contacto de los discos “0” y “2” con la barra “3”, y los puntos
E y F donde aquéllos establecen contacto con el sólido fijo “1”, se tendrá:
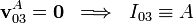
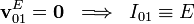
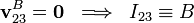
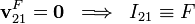
Aún quedan por obtener los C.I.R.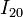 
e 
correspondientes al movimiento relativo del del disco pequeño respecto del grande, y al de la barra respecto del sólido fijo de referencia, respectivamente. La posición de estos puntos en el instante arbitrario reflejado en la figura puede ser fácilmente determinada mediante el teorema de los tres centros.
2.1 Aplicación del Teorema de los tres centros
Como sabemos, dicho teorema establece que si tres sólidos realizan movimientos relativos planos, con idéntico plano director, las posiciones que ocupan los C.I.R. en un instante están alineadas. En el sistema bajo estudio esto significa que el C.I.R. del movimiento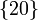 
(punto 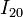) debe estar en la misma recta que los de los movimientos 
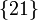y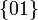 
; es decir, en el instante de la figura debe estar en la recta Δ(E,F), definida por los puntos E y F. Pero, simultáneamente, 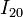debe pertenecer a la recta Δ(A,B), que pasa por los puntos de contacto A y B, pues son las posiciones de los C.I.R. de los movimientos 
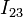y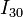 
. Por tanto, el C.I.R. 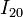se encuentra en la intersección de dichas rectas (ver figura):
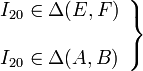
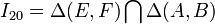
Anáologamente, el C.I.R. del movimiento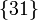 
(punto ) debe estar alineado con los puntos A y E, al coincidir éstos con los C.I.R. de los movimientos 
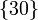y 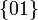(recuérdese que 
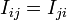). Pero además, dicho punto debe estar en la recta Δ(A,F), que pasa por los centros de los movimientos 
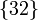y .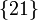
