Dos discos y barra rodando sin deslizar
De Laplace
(Diferencias entre revisiones)
(→Enunciado) |
(→Enunciado) |
||
| Línea 4: | Línea 4: | ||
# Determine los C.I.R. de los diferentes movimientos relativos en el sistema descrito. ¿Cómo es el movimiento instantáneo de la barra “3” respecto del sólido fijo “1”? | # Determine los C.I.R. de los diferentes movimientos relativos en el sistema descrito. ¿Cómo es el movimiento instantáneo de la barra “3” respecto del sólido fijo “1”? | ||
| - | # Suponiendo que en el movimiento del disco de mayor radio respecto del sólido fijo la velocidad de su centro <math>C</math> es un vector constante de valor conocido <math>\mathbf{v}_0</math>, determine las reducciones cinemáticas de | + | # Suponiendo que en el movimiento del disco de mayor radio respecto del sólido fijo la velocidad de su centro <math>C</math> es un vector constante de valor conocido <math>\mathbf{v}_0</math>, determine las reducciones cinemáticas de los movimientos \{01\}, \{21\} y \{31\}. |
| - | los movimientos \{01\}, \{21\} y \{31\}. | + | |
# Determine la ley horaria que sigue la distancia <math>\displaystyle\Delta x</math> entre los puntos de contacto de los discos con el sólido fijo. Supóngase que en el instante inicial esta distancia es <math>3R</math>. | # Determine la ley horaria que sigue la distancia <math>\displaystyle\Delta x</math> entre los puntos de contacto de los discos con el sólido fijo. Supóngase que en el instante inicial esta distancia es <math>3R</math>. | ||
Revisión de 23:06 14 sep 2010
Enunciado
Sendos discos de radios radios 2R y R (sólidos “0” y “2”, respectivamente) se encuentran siempre contenidos en el mismo plano y en contacto puntual sobre el sólido fijo “1”. Además, hay una barra rígida (sólido “3”), también contenida en el plano de los discos y en contacto puntual con éstos. El sistema se mueve de manera que los discos “0” y “2” ruedan sin deslizar de manera simultánea sobre los sólidos “1” y “3”.
- Determine los C.I.R. de los diferentes movimientos relativos en el sistema descrito. ¿Cómo es el movimiento instantáneo de la barra “3” respecto del sólido fijo “1”?
- Suponiendo que en el movimiento del disco de mayor radio respecto del sólido fijo la velocidad de su centro C es un vector constante de valor conocido
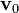, determine las reducciones cinemáticas de los movimientos \{01\}, \{21\} y \{31\}.
- Determine la ley horaria que sigue la distancia
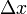entre los puntos de contacto de los discos con el sólido fijo. Supóngase que en el instante inicial esta distancia es 3R.
- Determine la reducción cinemática del movimiento relativo del disco pequeño respecto del grande, \{20\}. Calcule la aceleración instantánea del centro D en dicho movimiento.
