Problemas de vectores libres (G.I.T.I.)
De Laplace
(→Seno y coseno de una suma) |
(→Teoremas del seno y del coseno) |
||
| Línea 43: | Línea 43: | ||
Con ayuda de productos escalares y vectoriales demuestre los teoremas del coseno | Con ayuda de productos escalares y vectoriales demuestre los teoremas del coseno | ||
| - | <center><math>c^2 = a^2 + b^2 -2ab\,cos(\gamma)</math> | + | <center><math>c^2 = a^2 + b^2 -2ab\,cos(\gamma)</math></center> |
y del seno | y del seno | ||
| + | |||
<center><math>\frac{\mathrm{sen}\,\alpha}{a}=\frac{\mathrm{sen}\,\beta}{b}=\frac{\mathrm{sen}\,\gamma}{c}</math></center> | <center><math>\frac{\mathrm{sen}\,\alpha}{a}=\frac{\mathrm{sen}\,\beta}{b}=\frac{\mathrm{sen}\,\gamma}{c}</math></center> | ||
Revisión de 16:40 14 sep 2010
Contenido[ocultar] |
1 Formulas posiblemente incorrectas
De las siguientes expresiones, indique cuáles son necesariamente incorrectas. Aquí las diferentes letras representan las magnitudes definidas en el problema de ejemplos de análisis dimensional, R es una distancia y  el vector de posición; t es el tiempo:
el vector de posición; t es el tiempo:
- (a)
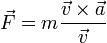
- (b)
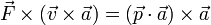
- (c)
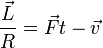
- (d)
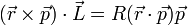
- (e)
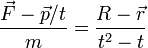
- (f)
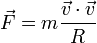
- (g)

- (h)
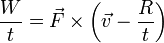
2 Ejemplo de clasificación de vectores
De los sigueinetes vectores ligados con sus respectivos puntos de aplicación:
- a)
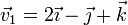 en
en 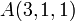
- b)
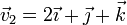 en
en 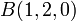
- c)
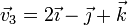 en
en 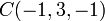
- d)
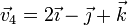 en
en 
- e)
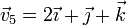 en
en 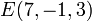
indique cuáles pueden representar al mismo vector deslizante y cuáles al mismo vector libre.
3 Arco capaz
Sean A y B dos puntos diametralmente opuestos en una circunferencia c. Sea P otro punto de la misma circunferencia. Demuestre que los vectores \overrightarrow{AP} y \overrightarrow{BP} son ortogonales.
Inversamente, sean A, B y P tres puntos tales que 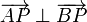 . Sea C el punto medio entre A y B. Pruebe que
. Sea C el punto medio entre A y B. Pruebe que 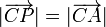
4 Diagonales de un rombo
Demuestre que las diagonales de un rombo son perpendiculares entre sí.
5 Seno y coseno de una diferencia
A partir del producto escalar y del vectorial de dos vectores del plano, con módulo unidad, demuestre las fórmulas trigonométricas para el coseno y el seno de una diferencia de dos ángulos.
6 Teoremas del seno y del coseno
Con ayuda de productos escalares y vectoriales demuestre los teoremas del coseno
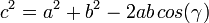
y del seno
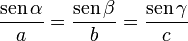
en un triángulo de lados a, b y c y ángulos opuestos α, β y γ.
7 Ejemplo de construcción de una base
Dados los vectores
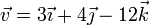
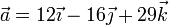
Construya una base ortonormal dextrógira, tal que
- El primer vector vaya en la dirección de

- El segundo esté contenido en el plano definido por
 y
y 
- El tercero sea perpendicular a los dos anteriores, y orientado según la regla de la mano derecha.
8 Base dual
Sea 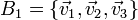 una base vectorial arbitraria. Sean
una base vectorial arbitraria. Sean 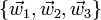 tres vectores definidos por
tres vectores definidos por
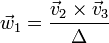
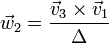


- 1. Demuestre que el conjunto
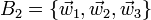 es también una base (llamada base dual de B1). ¿Cuánto vale el producto mixto de sus vectores?
es también una base (llamada base dual de B1). ¿Cuánto vale el producto mixto de sus vectores?
- 2. Pruebe que se cumple
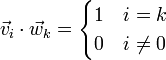
- 3. Demuestre que las componentes de un vector en la base B1 pueden calcularse proyectando sobre la base B2, esto es, si
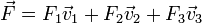
- la componente k viene dada por
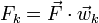
- 4. Halle la base dual de la base
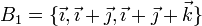
- 5. Calcule las componentes del vector
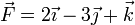
- en la base del apartado anterior.





