Entrar Página Discusión Historial Go to the site toolbox

Carga de un condensador parcialmente relleno

De Laplace

(Diferencias entre revisiones)
(→Solución)
(→Campos inmediatamente después de la conexión)
Línea 44: Línea 44:
===Campos inmediatamente después de la conexión===
===Campos inmediatamente después de la conexión===
-
En el instante $t=0^+$, ya se han establecido los campos iniciales,
+
En el instante $t=0^+$, ya se han establecido los campos iniciales, pero aún no hay tiempo para la acumulación de carga en el interior del sistema. En este instante $\sigma_s=0$ y el sistema se reduce a
-
pero aún no hay tiempo para la acumulación de carga en el interior
+
 
-
del sistema. En este instante $\sigma_s=0$ y el sistema se reduce a
+
<center><math>aE_1+bE_2=V_0\qquad \varepsilon_0E_2=\varepsilon E_1\,</math></center>
-
\[
+
 
-
aE_1+bE_2=V_0\qquad \varepsilon_2E_2=\varepsilon_1E_1
+
-
\]
+
La solución de este sistema es
La solución de este sistema es
-
\[
+
<center> <math>E_1=\frac{V_0\varepsilon_0}{\varepsilon b+\varepsilon_0 a}
-
E_1=\frac{V_0\varepsilon_2}{\varepsilon_1b+\varepsilon_2a}
+
\qquad
\qquad
-
E_2=\frac{V_0\varepsilon_1}{\varepsilon_1b+\varepsilon_2a}
+
E_2=\frac{V_0\varepsilon }{\varepsilon b+\varepsilon_0 a}</math></center>
-
\]
+
 
-
Esta distribución de campos es la misma que habría si los medios
+
Esta distribución de campos es la misma que habría si los medios fueran dieléctricos perfectos.
-
fueran dieléctricos perfectos.
+
 
 +
El vector desplazamiento es, en las dos regiones,
 +
 
 +
<math>\mathbf{D}_1=\mathbf{D}_2=\frac{\varepsilon \varepsilon_0V_0}{\varepsilon b+\varepsilon_0 a}\mathbf{u}_z</math>
 +
 
 +
Las únicas cargas son las acumuladas en las placas. En la placa superior tenemos
 +
 
 +
<center><math>Q_2=\oint
 +
\mathbf{D}_2{\cdot}\mathrm{d}\mathbf{S}=-\frac{\varepsilon \varepsilon_0V_0S}{\varepsilon b+\varepsilon_0a}
 +
</math></center>
-
El vector desplazamiento es, en las dos regiones
 
-
\[
 
-
D_1=D_2=\frac{\varepsilon_1\varepsilon_2V_0}{\varepsilon_1b+\varepsilon_2a}
 
-
\]
 
-
Las únicas cargas son las acumuladas en las placas. En la placa
 
-
superior tenemos
 
-
\[
 
-
Q_2=\oint
 
-
\mathbf{D}_2{\cdot}\mathrm{d}\mathbf{S}=-\frac{\varepsilon_1\varepsilon_2V_0S}{\varepsilon_1b+\varepsilon_2a}
 
-
\]
 
En la inferior la carga es la misma, salvo el signo
En la inferior la carga es la misma, salvo el signo
-
\[
+
 
-
Q_1=\oint
+
<center><math>Q_1=\oint
-
\mathbf{D}_1{\cdot}\mathrm{d}\mathbf{S}=\frac{\varepsilon_1\varepsilon_2V_0S}{\varepsilon_1b+\varepsilon_2a}
+
\mathbf{D}_1{\cdot}\mathrm{d}\mathbf{S}=\frac{\varepsilon \varepsilon_0V_0S}{\varepsilon b+\varepsilon_0a}</math></center>
-
\]
+
 
En la interfaz no hay carga acumulada todavía.
En la interfaz no hay carga acumulada todavía.
-
\[
+
 
-
Q_s=\oint\mathbf{D}{\cdot}\mathrm{d}\mathbf{S}=D_2 S-D_1S=0
+
<center><math>Q_s=\oint\mathbf{D}{\cdot}\mathrm{d}\mathbf{S}=D_2 S-D_1S=0</math></center>
-
\]
+
 
-
Aunque todavía no haya carga acumulada, ya está fluyendo
+
Aunque todavía no haya carga acumulada, ya está fluyendo corriente de una placa a través del material. La corriente en cada región es
-
corriente de una placa hacia la otra. La corriente en cada
+
 
-
región es
+
<center><math>\mathbf{J}_1=\sigma \mathbf{E}_1=\frac{\sigma_1\varepsilon_0V_0}{\varepsilon b+\varepsilon_0a}\mathbf{u}_z</math></center>
-
\[
+
 
-
J_1=\sigma_1E_1=\frac{\sigma_1\varepsilon_2V_0}{\varepsilon_1b+\varepsilon_2a}
+
<center><math>\mathbf{J}_2=\sigma_2 \mathbf{E}_2= \mathbf{0}\,</math></center>
-
\qquad
+
 
-
%\]\[
+
Al ser diferentes estas corrientes, la carga en la interfaz varía a un ritmo
-
J_2=\sigma_2E_2=\frac{\sigma_2\varepsilon_1V_0}{\varepsilon_1b+\varepsilon_2a}
+
 
-
\]
+
<math>\left.\frac{\partial \sigma_s}{\partial t}\right|_{t=0^+}=-\mathbf{n}{\cdot}[\mathbf{J}]=J_1-J_2
-
Al ser diferentes estas corrientes, la carga en la interfaz varía a
+
=\frac{\sigma \varepsilon_0V_0}{\varepsilon b+\varepsilon_0a}
-
un ritmo
+
</math>
-
\[
+
-
\left.\frac{\partial \sigma_s}{\partial t}\right|_{t=0^+}=-\mathbf{n}{\cdot}[\mathbf{J}]=J_1-J_2
+
-
=\frac{(\sigma_1\varepsilon_2-\sigma_2\varepsilon_1)V_0}{\varepsilon_1b+\varepsilon_2a}
+
-
\]
+
===Campos en el estado estacionario===
===Campos en el estado estacionario===

Revisión de 11:36 7 jun 2008

Contenido

1 Enunciado

Entre dos placas planas y paralelas separadas una distancia a + b se coloca una capa de espesor a de un medio de permitividad \varepsilon y conductividad σ. El resto del espacio lo ocupa una capa de espesor b vacía.

En el instante t = 0 se conecta una diferencia de potencial V0.

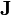  1. ¿Cuánto valen \mathbf{E}, \mathbf{D} y \mathbf{J} inmediatamente después de conectar el potencial?
  2. ¿Cuánto valen un tiempo largo después de que se haya establecido?
  3. ¿Cuánto valen en cualquier instante?
  4. ¿Cómo varía, durante el periodo transitorio, la energía almacenada en el sistema? ¿Cuánta energía se disipa durante este periodo? ¿De dónde procede esta energía?
  5. Si en lugar de una tensión escalón se aplica durante un largo periodo de tiempo un voltaje alterno V = V0cos(ωt)
    1. ¿Cuánto vale la corriente que llega al elemento? ¿Cuál es la impedancia del sistema? ¿Y el circuito equivalente?
    2. ¿Cuanto vale la energía aportada por el generador en un periodo? ¿En qué se emplea esta energía?

2 Solución

Por la simetría del sistema, si despreciamos los efectos de borde, podemos admitir que los campos son uniformes en cada región aunque podrán, en principio, depender del tiempo.

Desde el instante t = 0 + la diferencia de potencial entre las placas está fijada en $V_0$, por lo que siempre se verificará

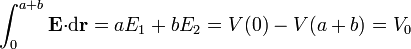
\int_0^{a+b}\mathbf{E}{\cdot}\mathrm{d}\mathbf{r}=aE_1+bE_2=V(0)-V(a+b)=V_0

Por otro lado, en la interfaz podrá haber una carga acumulada, lo que hace que el vector desplazamiento sea discontinuo

\mathbf{n}{\cdot}[\mathbf{D}]=\sigma_s\quad\Rightarrow\quad \varepsilon_0E_2-\varepsilon E_1=\sigma_s

Esta carga aparece debido a la presencia de conductividad en el medio, que posibilita que fluya carga por su interior. Esta carga acumulada es también una incógnita del problema. No conocemos cuanto vale, pero sí como varía, ya que la acumulación de carga verifica

\mathbf{n}{\cdot}[\mathbf{J}]=-\frac{\partial \sigma_s}{\partial t}\quad\Rightarrow\quad \sigma_2E_2-\sigma_1E_1=-\frac{\partial \sigma_s}{\partial t}

El sistema de ecuaciones resultante

aE_1+bE_2=V_0\,


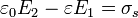
\varepsilon_0E_2-\varepsilon E_1=\sigma_s\,


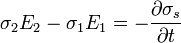
\sigma_2E_2-\sigma_1E_1=-\frac{\partial \sigma_s}{\partial t}


posee solución en general, que se verá más adelante. Primero, consideraremos dos casos límite.


2.1 Campos inmediatamente después de la conexión

En el instante $t=0^+$, ya se han establecido los campos iniciales, pero aún no hay tiempo para la acumulación de carga en el interior del sistema. En este instante $\sigma_s=0$ y el sistema se reduce a

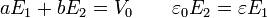
aE_1+bE_2=V_0\qquad \varepsilon_0E_2=\varepsilon E_1\,

La solución de este sistema es

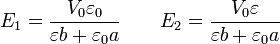
E_1=\frac{V_0\varepsilon_0}{\varepsilon b+\varepsilon_0 a} \qquad E_2=\frac{V_0\varepsilon }{\varepsilon b+\varepsilon_0 a}

Esta distribución de campos es la misma que habría si los medios fueran dieléctricos perfectos.

El vector desplazamiento es, en las dos regiones,

\mathbf{D}_1=\mathbf{D}_2=\frac{\varepsilon \varepsilon_0V_0}{\varepsilon b+\varepsilon_0 a}\mathbf{u}_z

Las únicas cargas son las acumuladas en las placas. En la placa superior tenemos

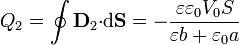
Q_2=\oint \mathbf{D}_2{\cdot}\mathrm{d}\mathbf{S}=-\frac{\varepsilon \varepsilon_0V_0S}{\varepsilon b+\varepsilon_0a}

En la inferior la carga es la misma, salvo el signo

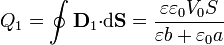
Q_1=\oint \mathbf{D}_1{\cdot}\mathrm{d}\mathbf{S}=\frac{\varepsilon \varepsilon_0V_0S}{\varepsilon b+\varepsilon_0a}

En la interfaz no hay carga acumulada todavía.

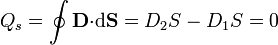
Q_s=\oint\mathbf{D}{\cdot}\mathrm{d}\mathbf{S}=D_2 S-D_1S=0

Aunque todavía no haya carga acumulada, ya está fluyendo corriente de una placa a través del material. La corriente en cada región es

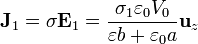
\mathbf{J}_1=\sigma \mathbf{E}_1=\frac{\sigma_1\varepsilon_0V_0}{\varepsilon b+\varepsilon_0a}\mathbf{u}_z
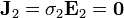
\mathbf{J}_2=\sigma_2 \mathbf{E}_2= \mathbf{0}\,

Al ser diferentes estas corrientes, la carga en la interfaz varía a un ritmo

\left.\frac{\partial \sigma_s}{\partial t}\right|_{t=0^+}=-\mathbf{n}{\cdot}[\mathbf{J}]=J_1-J_2 =\frac{\sigma \varepsilon_0V_0}{\varepsilon b+\varepsilon_0a}

2.2 Campos en el estado estacionario

2.3 Evolución en el periodo transitorio

2.4 Potencia y energía durante el periodo transitorio

2.5 Comportamiento en corriente alterna

2.5.1 Corriente, impedancia y circuito equivalente

2.5.2 Energía en corriente alterna

Obtenido de "http://tesla.us.es/wiki/index.php/Carga_de_un_condensador_parcialmente_relleno"

Herramientas:

Herramientas personales
TOOLBOX
LANGUAGES
licencia de Creative Commons
 Aviso legal - Acerca de Laplace