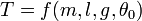1.4. Dependencias del periodo de un péndulo
De Laplace
(Diferencias entre revisiones)
(Página creada con '==Enunciado== Un péndulo simple es una masa <math>m</math> suspendida de un hilo ideal (sin masa), que tiene una longitud <math>l</math>. La masa está sometida a la aceleraci…') |
(→Posibles dependencias) |
||
| Línea 5: | Línea 5: | ||
==Posibles dependencias== | ==Posibles dependencias== | ||
| - | El periodo del péndulo solo puede depender de aquellas magnitudes que definen el problema: la longitud del hilo, <math>l</math>; la aceleración de la gravedad, <math>g</math>; la masa <math>m</math>; y la amplitud inicial con la que se separa de la vertical. | + | El periodo del péndulo solo puede depender de aquellas magnitudes que definen el problema: la longitud del hilo, <math>l</math>; la aceleración de la gravedad, <math>g</math>; la masa <math>m</math>; y la amplitud inicial con la que se separa de la vertical,<math>\theta_0</math>. |
| + | |||
| + | <center><math>T = f(m,l,g,\theta_0)\,</math></center> | ||
| + | |||
==Casos prácticos== | ==Casos prácticos== | ||
[[Categoría:Problemas de metrología]] | [[Categoría:Problemas de metrología]] | ||
Revisión de 10:17 9 sep 2010
1 Enunciado
Un péndulo simple es una masa m suspendida de un hilo ideal (sin masa), que tiene una longitud l. La masa está sometida a la aceleración de la gravedad, g.
Si duplicamos la longitud del péndulo, ¿cómo cambiará su periodo de oscilación? ¿Y si nos llevamos el péndulo a la Luna, donde la gravedad es 1/6 de la terrestre?
2 Posibles dependencias
El periodo del péndulo solo puede depender de aquellas magnitudes que definen el problema: la longitud del hilo, l; la aceleración de la gravedad, g; la masa m; y la amplitud inicial con la que se separa de la vertical,θ0.