1.1. Ejemplos de análisis dimensional
De Laplace
(Diferencias entre revisiones)
(Página creada con '==Enunciado== A partir de las relaciones definitorias {| class="bordeado" |- ! Velocidad ! Cantidad de movimiento ! Aceleración ! Fuerza |- | <math>\vec{v}=\frac{\mathrm{d}\ve…') |
(→Velocidad) |
||
| Línea 28: | Línea 28: | ||
==Velocidad== | ==Velocidad== | ||
| + | La velocidad se define como la derivada de la posición respecto al tiempo. Una derivada no es más que un cociente entre dos cantidades muy pequeñas y por tanto sus dimensiones serán las del numerador divididas por las del denominador, esto es, | ||
| + | |||
| + | <center><math>[v] = \frac{[r]}{[t} = L T^{-1}</math></center> | ||
| + | |||
==Cantidad de movimiento== | ==Cantidad de movimiento== | ||
==Aceleración== | ==Aceleración== | ||
Revisión de 14:21 8 sep 2010
Contenido |
1 Enunciado
A partir de las relaciones definitorias
| Velocidad | Cantidad de movimiento | Aceleración | Fuerza |
|---|---|---|---|
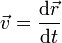
| 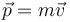
| 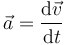
| 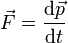
|
| Trabajo | Potencia | Momento cinético | Momento de una fuerza |
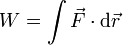
| 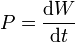
| 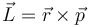
| 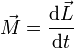
|
determine las ecuaciones dimensionales de estas magnitudes, así como sus unidades en el SI en función de las unidades fundamentales de este sistema.
2 Velocidad
La velocidad se define como la derivada de la posición respecto al tiempo. Una derivada no es más que un cociente entre dos cantidades muy pequeñas y por tanto sus dimensiones serán las del numerador divididas por las del denominador, esto es,
![[v] = \frac{[r]}{[t} = L T^{-1}](/wiki/images/math/9/6/e/96edfb3c0d425fee36517ee1bcb2335a.png)





