Movimiento helicoidal de un sólido rígido

De Laplace

(Diferencias entre revisiones)

Revisión de 20:53 27 jul 2010

Contenido

1 Introducción
2 Eje instantáneo de rotación y mínimo deslizamiento
3 Celeridad de un punto
4 Componente paralela de la velocidad
5 Dirección y sentido de la velocidad
6 Generalidad del movimiento helicoidal

1 Introducción

El campo de velocidades de un sólido rígido tiene la forma

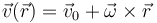
$\vec{v}(\vec{r}) = \vec{v}_0+\vec{\omega}\times\vec{r}$

El movimiento helicoidal instantáneo se da cuando ni $\vec{v}_0$ ni $\vec{\omega}$ son nulos, pero sí paralelos:

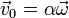
$\vec{v}_0 = \alpha\vec{\omega}$

Este campo de velocidades posee una serie de propiedades:

Existe una recta, paralela a la velocidad angular, tal que la velocidad de sus puntos posee módulo mínimo y dirección la de la propia recta (eje instantáneo de rotación y mínimo deslizamiento, EIRMD).
El EIRMD pasa por el origen de coordenadas y tiene la dirección de la velocidad angular.
Todos los puntos situados a la misma distancia de este eje poseen la misma celeridad.
La proyección de la velocidad de cada punto sobre la velocidad angular es la misma para todos los puntos.
La velocidad de todos los puntos situados a la misma distancia forma el mismo ángulo con la velocidad angular.
El sentido de la velocidad cumple la regla de la mano derecha respecto a la velocidad angular.

2 Eje instantáneo de rotación y mínimo deslizamiento

Consideremos en primer lugar la velocidad del origen de coordenadas.

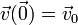
$\vec{v}(\vec{0}) = \vec{v}_0$

Por tanto $\vec{v}_0$ representa la velocidad con la que se mueve el origen de coordenadas.

Si ahora consideramos un punto situado en la recta que pasa por el origen y con la dirección dada por la velocidad angular

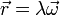
$\vec{r}=\lambda\vec{\omega}$

La velocidad de estos puntos es

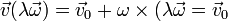
$\vec{v}(\lambda\vec{\omega})=\vec{v}_0+\omega\times(\lambda\vec{\omega}=\vec{v}_0$

esto es, todos se mueven con la misma velocidad y además esta velocidad va en la dirección de la recta que une los puntos.

3 Celeridad de un punto

Si ahora consideramos un punto fuera de esta recta y situado a una distancia $d$ de ella, su velocidad será

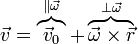
$\vec{v}=\overbrace{\vec{v}_0}^{\parallel\vec{\omega}} +\overbrace{\vec{\omega}\times\vec{r}}^{\perp\vec{\omega}}$

Al ser las dos componentes perpendiculares entre sí, el módulo de este vector es

$v = \sqrt{v_0^2+ |\vec{\omega}\times\vec{r}|} = \sqrt{v_0^2+\omega^2d^2}$

De este resultado extraemos dos conclusiones:

Todos los puntos situados a la misma distancia del eje tienen la misma celeridad.
Esta celeridad es mínima en el propio eje ( $d = 0$ ).

4 Componente paralela de la velocidad

La proyección de la velocidad en la dirección de la velocidad angular es

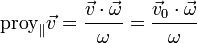
$\mathrm{proy}_\parallel\vec{v}=\frac{\vec{v}\cdot\vec{\omega}}{\omega}=\frac{\vec{v}_0\cdot\vec{\omega}}{\omega}$

Al depender solo de los vectores $\vec{v}_0$ y $\vec{\omega}$ , esta proyección es la misma para todos los puntos. En este caso, además, al tratarse vectores paralelos

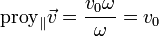
$\mathrm{proy}_\parallel\vec{v}=\frac{v_0\omega}{\omega}=v_0$

5 Dirección y sentido de la velocidad

En cuanto al ángulo que forma la velocidad con la velocidad angular tenemos

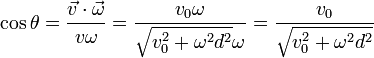
$\cos\theta = \frac{\vec{v}\cdot\vec{\omega}}{v\omega}=\frac{v_0\omega}{\sqrt{v_0^2+\omega^2d^2}\omega}=\frac{v_0}{\sqrt{v_0^2+\omega^2d^2}}$

Equivalentemente, el ángulo verifica

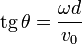
$\mathrm{tg}\,\theta = \frac{\omega d}{v_0}$

Este ángulo es nulo si $d = 0$ , lo que de nuevo nos dice que en los puntos del eje la velocidad es paralela a la velocidad angular. A medida

Como en el caso de la rotación pura, dos puntos situados sobre la misma vertical tienen la misma velocidad, aunque en este caso el movimiento no esté limitado a un plano.

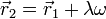
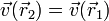
$\vec{r}_2 = \vec{r}_1+\lambda\omega$ $\Rightarrow$ $\vec{v}(\vec{r}_2)=\vec{v}(\vec{r}_1)$

Por último, el sentido de la velocidad cumple la regla de la mano derecha respecto a la velocidad angular.

Este movimiento se denomina movimiento helicoidal (o de tornillo) porque si uno traza las líneas de corriente (tangentes a la velocidad en cada punto), obtiene hélices que avanzan a la vez que giran en torno al EIRMD. Esto NO quiere decir que el movimiento de cada partícula sea helicoidal, ya que

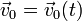
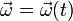
$\vec{v}_0=\vec{v}_0(t)$ $\vec{\omega}=\vec{\omega}(t)$

y por tanto, el EIRMD y la dirección de la velocidad de cada partícula puede cambiar continuamente.

6 Generalidad del movimiento helicoidal

@@ Línea 17: / Línea 17: @@
 * El sentido de la velocidad cumple la regla de la mano derecha respecto a la velocidad angular.
+==Eje instantáneo de rotación y mínimo deslizamiento==
 Consideremos en primer lugar la velocidad del origen de coordenadas.
@@ Línea 33: / Línea 34: @@
 esto es, todos se mueven con la misma velocidad y además esta velocidad va en la dirección de la recta que une los puntos.
+==Celeridad de un punto==
 Si ahora consideramos un punto fuera de esta recta y situado a una distancia <math>d</math> de ella, su velocidad será
@@ Línea 46: / Línea 48: @@
 * Esta celeridad es mínima en el propio eje (<math>d=0</math>).
+==Componente paralela de la velocidad==
 La proyección de la velocidad en la dirección de la velocidad angular es
@@ Línea 54: / Línea 57: @@
 <center><math>\mathrm{proy}_\parallel\vec{v}=\frac{v_0\omega}{\omega}=v_0</math></center>
+==Dirección y sentido de la velocidad==
 En cuanto al ángulo que forma la velocidad con la velocidad angular tenemos
@@ Línea 76: / Línea 80: @@
 y por tanto, el EIRMD y la dirección de la velocidad de cada partícula puede cambiar continuamente.
+==Generalidad del movimiento helicoidal==
 [[Categoría:Cinemática del sólido rígido]]

Movimiento helicoidal de un sólido rígido

De Laplace

Revisión de 20:53 27 jul 2010

Contenido

1 Introducción

2 Eje instantáneo de rotación y mínimo deslizamiento

3 Celeridad de un punto

4 Componente paralela de la velocidad

5 Dirección y sentido de la velocidad

6 Generalidad del movimiento helicoidal

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES