Entrar Página Discusión Historial Go to the site toolbox

Teorema de Chasles

De Laplace

(Diferencias entre revisiones)
(→Deducción de la forma del campo)
Línea 34: Línea 34:
==Deducción de la forma del campo==
==Deducción de la forma del campo==
-
Más complicado es el recíproco: que si verifica la condición cinemática de rigidez, de
+
Más complicado es el recíproco: que si verifica la condición cinemática de rigidez, la forma general del campo de velocidades es la indicada.
-
La condición de equiproyectividad para un campo vectorial <math>\vec{v}(\vec{r})</math> puede expresarse como que para cualesquiera dos puntos <math>\vec{r}_1</math> y <math>\vec{r}_2</math> se verifica
+
 
 +
La condición cinemática de rigidiez equivale a la equiproyectividad del campo de velocidades: para cualesquiera dos puntos <math>\vec{r}_1</math> y <math>\vec{r}_2</math> se verifica
<center><math>\vec{v}(\vec{r}_1)\cdot\left(\vec{r}_2-\vec{r}_1\right)= \vec{v}(\vec{r}_2)\cdot\left(\vec{r}_2-\vec{r}_1\right)</math></center>
<center><math>\vec{v}(\vec{r}_1)\cdot\left(\vec{r}_2-\vec{r}_1\right)= \vec{v}(\vec{r}_2)\cdot\left(\vec{r}_2-\vec{r}_1\right)</math></center>
Línea 45: Línea 46:
Para demostrarlo, suponemos un sistema de referencia con origen en el punto <math>\vec{0}</math> y cuyos ejes vienen caracterizados por los vectores unitarios <math>\vec{\imath}</math>, <math>\vec{\jmath}</math> y <math>\vec{k}</math>.
Para demostrarlo, suponemos un sistema de referencia con origen en el punto <math>\vec{0}</math> y cuyos ejes vienen caracterizados por los vectores unitarios <math>\vec{\imath}</math>, <math>\vec{\jmath}</math> y <math>\vec{k}</math>.
-
====Referencia al origen====
+
===Veolicdad relativa al origen===
-
Definamos en primer lugar el campo, también equiproyectivo
+
Definamos en primer lugar el campo de velocidades, también equiproyectivo
<center><math>\vec{u}(\vec{r}) = \vec{v}(\vec{r})-\vec{v}(\vec{0})</math></center>
<center><math>\vec{u}(\vec{r}) = \vec{v}(\vec{r})-\vec{v}(\vec{0})</math></center>
 +
 +
que representa la velocidad medida por un sistema que se mueve con la misma velocidad que el origen de coordenadas.
Este campo cumple
Este campo cumple
Línea 54: Línea 57:
<center><math>\vec{u}(\vec{r}_1)\cdot\left(\vec{r}_2-\vec{r}_1\right)= \vec{u}(\vec{r}_2)\cdot\left(\vec{r}_2-\vec{r}_1\right)</math>{{qquad}}{{qquad}}<math>\vec{u}(\vec{0})=\vec{0}</math></center>
<center><math>\vec{u}(\vec{r}_1)\cdot\left(\vec{r}_2-\vec{r}_1\right)= \vec{u}(\vec{r}_2)\cdot\left(\vec{r}_2-\vec{r}_1\right)</math>{{qquad}}{{qquad}}<math>\vec{u}(\vec{0})=\vec{0}</math></center>
-
====Equiproyectividad aplicada a cada vector de la base con el origen====
 
 +
===Equiproyectividad aplicada a cada vector de la base con el origen===
Si aplicamos la condición de equiproyectividad de <math>\vec{u}</math> a los dos puntos <math>\vec{r}_1=\vec{\imath}</math> y <math>\vec{r}_2=\vec{0}</math> nos queda
Si aplicamos la condición de equiproyectividad de <math>\vec{u}</math> a los dos puntos <math>\vec{r}_1=\vec{\imath}</math> y <math>\vec{r}_2=\vec{0}</math> nos queda
<center><math>\vec{u}(\vec{\imath})\cdot\vec{\imath} = \vec{u}(\vec{0})\cdot\vec{\imath} = 0</math></center>
<center><math>\vec{u}(\vec{\imath})\cdot\vec{\imath} = \vec{u}(\vec{0})\cdot\vec{\imath} = 0</math></center>
-
esto quiere decir que <math>\vec{u}(\vec{\imath})</math> es ortogonal a <math>\vec{\imath}</math>, esto es, no posee componente <math>X</math> y puede escribirse como
+
esto quiere decir que la velocidad <math>\vec{u}(\vec{\imath})</math> es ortogonal al vector de posición<math>\vec{\imath}</math>, esto es, no posee componente <math>X</math> y puede escribirse como
<center><math>\vec{u}(\vec{\imath}) = a\vec{\jmath} + b\vec{k}</math></center>
<center><math>\vec{u}(\vec{\imath}) = a\vec{\jmath} + b\vec{k}</math></center>
Línea 68: Línea 71:
<center><math>\vec{u}(\vec{\jmath}) = c\vec{\imath} + d\vec{k}</math>{{qquad}}{{qquad}}<math>\vec{u}(\vec{k}) = e\vec{\imath} + f\vec{\jmath}</math></center>
<center><math>\vec{u}(\vec{\jmath}) = c\vec{\imath} + d\vec{k}</math>{{qquad}}{{qquad}}<math>\vec{u}(\vec{k}) = e\vec{\imath} + f\vec{\jmath}</math></center>
-
====Equiproyectividad aplicada a pares de vectores de la base====
+
===Equiproyectividad aplicada a pares de vectores de la base====
La condición de equiproyectividad también puede aplicarse al par de puntos <math>\vec{\imath}</math> y <math>\vec{\jmath}</math>. En este caso tenemos
La condición de equiproyectividad también puede aplicarse al par de puntos <math>\vec{\imath}</math> y <math>\vec{\jmath}</math>. En este caso tenemos
Línea 86: Línea 89:
<center><math>\vec{u}(\vec{\imath}) = \omega_z\vec{\jmath}-\omega_y\vec{k}</math>{{qquad}}{{qquad}}<math>\vec{u}(\vec{\jmath}) = -\omega_z\vec{\imath}+\omega_x\vec{k}</math>{{qquad}}{{qquad}}<math>\vec{u}(\vec{k}) = \omega_y\vec{\imath}-\omega_x\vec{\jmath}</math></center>
<center><math>\vec{u}(\vec{\imath}) = \omega_z\vec{\jmath}-\omega_y\vec{k}</math>{{qquad}}{{qquad}}<math>\vec{u}(\vec{\jmath}) = -\omega_z\vec{\imath}+\omega_x\vec{k}</math>{{qquad}}{{qquad}}<math>\vec{u}(\vec{k}) = \omega_y\vec{\imath}-\omega_x\vec{\jmath}</math></center>
-
====Aplicación a un punto genérico====
+
===Aplicación a un punto genérico===
Si ahora aplicamos la condición de equiproyectividad a un punto cualquiera  
Si ahora aplicamos la condición de equiproyectividad a un punto cualquiera  
Línea 95: Línea 98:
<center><math>\vec{u}(\vec{r})\cdot\vec{r}=\vec{u}(\vec{0})\cdot\vec{r}= 0</math></center>
<center><math>\vec{u}(\vec{r})\cdot\vec{r}=\vec{u}(\vec{0})\cdot\vec{r}= 0</math></center>
-
esto es, que el campo en cada punto es ortogonal al vector de posición de dicho punto.
+
esto es, que la velocidad en cada punto es ortogonal al vector de posición de dicho punto.
Si ahora aplicamos la condición al mismo punto <math>\vec{r}</math> y al punto <math>\vec{\imath}</math> tenemos
Si ahora aplicamos la condición al mismo punto <math>\vec{r}</math> y al punto <math>\vec{\imath}</math> tenemos
Línea 110: Línea 113:
<center><math>\vec{u}(\vec{r}) = \left(\omega_yz-\omega_zy\right)\vec{\imath}+\left(\omega_zx-\omega_xz\right)\vec{\jmath}+\left(\omega_xy-\omega_yx\right)\vec{k}=\left|\begin{matrix}\vec{\imath} & \vec{\jmath} & \vec{k} \\ \omega_x & \omega_y & \omega_z \\ x & y & z\end{matrix}\right|=\vec{\omega}\times\vec{r}</math></center>
<center><math>\vec{u}(\vec{r}) = \left(\omega_yz-\omega_zy\right)\vec{\imath}+\left(\omega_zx-\omega_xz\right)\vec{\jmath}+\left(\omega_xy-\omega_yx\right)\vec{k}=\left|\begin{matrix}\vec{\imath} & \vec{\jmath} & \vec{k} \\ \omega_x & \omega_y & \omega_z \\ x & y & z\end{matrix}\right|=\vec{\omega}\times\vec{r}</math></center>
-
y volviendo a nuestro campo original, <math>\vec{v}</math>
+
y volviendo a nuestro campo de velocidades original, <math>\vec{v}</math>
<center><math>\vec{v}(\vec{r})=\vec{v}(\vec{0}) +\vec{\omega}\times\vec{r}</math></center>
<center><math>\vec{v}(\vec{r})=\vec{v}(\vec{0}) +\vec{\omega}\times\vec{r}</math></center>
-
===Campo de momentos implica campo equiproyectivo===
+
con lo que se completa la demostración del teorema de Chasles.
 +
 
 +
[[Categoría:Cinemática del sólido rígido]]

Revisión de 16:37 26 jul 2010

Contenido

1 Enunciado del teorema

El campo de velocidades de un sólido, cumple la condición de rigidez

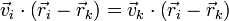
\vec{v}_i\cdot\left(\vec{r}_i-\vec{r}_k\right)=\vec{v}_k\cdot\left(\vec{r}_i-\vec{r}_k\right)

si y solo si es de la forma

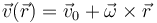
\vec{v}(\vec{r}) = \vec{v}_0+\vec{\omega}\times\vec{r}

esto es, se compone de una traslación y una rotación (que pueden ser nulas).

2 Verificación de la condición de rigidez

La demostración de que si el campo de velocidades es de la forma indicada, entonces cumple la condición de rigidez es bastante elemental. Si para todo 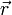\vec{r} se cumple

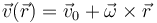
\vec{v}(\vec{r})=\vec{v}_0 +\vec{\omega}\times\vec{r}

entonces, para dos puntos cualesquiera se verifica

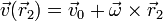
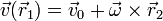
\vec{v}(\vec{r}_2)=\vec{v}_0 +\vec{\omega}\times\vec{r}_2    \vec{v}(\vec{r}_1)=\vec{v}_0 +\vec{\omega}\times\vec{r}_2

Restando

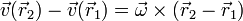
\vec{v}(\vec{r}_2)-\vec{v}(\vec{r}_1)=\vec{\omega}\times\left(\vec{r}_2-\vec{r}_1\right)

El segundo miembro es ortogonal a 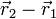\vec{r}_2-\vec{r}_1, por lo que

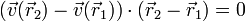
\left(\vec{v}(\vec{r}_2)-\vec{v}(\vec{r}_1)\right)\cdot\left(\vec{r}_2-\vec{r}_1\right)=0

y separando los términos

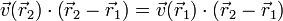
\vec{v}(\vec{r}_2)\cdot\left(\vec{r}_2-\vec{r}_1\right)=\vec{v}(\vec{r}_1)\cdot\left(\vec{r}_2-\vec{r}_1\right)

esto es, el campo de velocidades es equiproyectivo y cumple la condición de rigidez.

3 Deducción de la forma del campo

Más complicado es el recíproco: que si verifica la condición cinemática de rigidez, la forma general del campo de velocidades es la indicada.

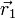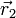La condición cinemática de rigidiez equivale a la equiproyectividad del campo de velocidades: para cualesquiera dos puntos \vec{r}_1 y \vec{r}_2 se verifica

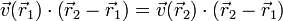
\vec{v}(\vec{r}_1)\cdot\left(\vec{r}_2-\vec{r}_1\right)= \vec{v}(\vec{r}_2)\cdot\left(\vec{r}_2-\vec{r}_1\right)

se trata de demostrar que si se cumple esta condición, 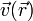\vec{v}(\vec{r}) puede escribirse en la forma

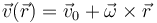
\vec{v}(\vec{r})=\vec{v}_0+\vec{\omega}\times\vec{r}

Para demostrarlo, suponemos un sistema de referencia con origen en el punto 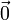\vec{0} y cuyos ejes vienen caracterizados por los vectores unitarios 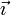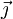\vec{\imath}, \vec{\jmath} y \vec{k}.

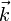3.1 Veolicdad relativa al origen

Definamos en primer lugar el campo de velocidades, también equiproyectivo

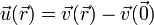
\vec{u}(\vec{r}) = \vec{v}(\vec{r})-\vec{v}(\vec{0})

que representa la velocidad medida por un sistema que se mueve con la misma velocidad que el origen de coordenadas.

Este campo cumple

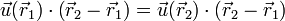
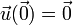
\vec{u}(\vec{r}_1)\cdot\left(\vec{r}_2-\vec{r}_1\right)= \vec{u}(\vec{r}_2)\cdot\left(\vec{r}_2-\vec{r}_1\right)        \vec{u}(\vec{0})=\vec{0}


3.2 Equiproyectividad aplicada a cada vector de la base con el origen

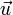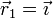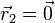Si aplicamos la condición de equiproyectividad de \vec{u} a los dos puntos \vec{r}_1=\vec{\imath} y \vec{r}_2=\vec{0} nos queda

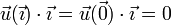
\vec{u}(\vec{\imath})\cdot\vec{\imath} = \vec{u}(\vec{0})\cdot\vec{\imath} = 0

esto quiere decir que la velocidad 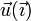\vec{u}(\vec{\imath}) es ortogonal al vector de posición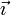\vec{\imath}, esto es, no posee componente X y puede escribirse como

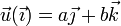
\vec{u}(\vec{\imath}) = a\vec{\jmath} + b\vec{k}

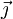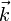Aplicando el mismo razonamiento a \vec{\jmath} y a \vec{k} nos queda

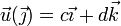
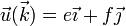
\vec{u}(\vec{\jmath}) = c\vec{\imath} + d\vec{k}        \vec{u}(\vec{k}) = e\vec{\imath} + f\vec{\jmath}

3.3 Equiproyectividad aplicada a pares de vectores de la base=

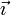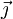La condición de equiproyectividad también puede aplicarse al par de puntos \vec{\imath} y \vec{\jmath}. En este caso tenemos

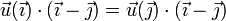
\vec{u}(\vec{\imath})\cdot\left(\vec{\imath}-\vec{\jmath}\right) = \vec{u}(\vec{\jmath})\cdot\left(\vec{\imath}-\vec{\jmath}\right)   \Rightarrow   -a = c\,

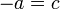
Operando igualmente con los otros dos pares nos queda

-b = e\,        -d = f\,

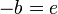
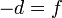
Si llamamos

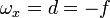
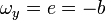
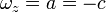
\omega_x = d = -f\,        \omega_y = e = -b\,        \omega_z = a = -c\,

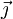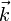el valor de \vec{u} en \vec{\imath}, \vec{\jmath} y \vec{k} se escribe

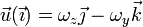
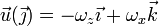
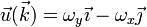
\vec{u}(\vec{\imath}) = \omega_z\vec{\jmath}-\omega_y\vec{k}        \vec{u}(\vec{\jmath}) = -\omega_z\vec{\imath}+\omega_x\vec{k}        \vec{u}(\vec{k}) = \omega_y\vec{\imath}-\omega_x\vec{\jmath}

3.4 Aplicación a un punto genérico

Si ahora aplicamos la condición de equiproyectividad a un punto cualquiera

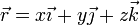
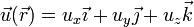
\vec{r}=x\vec{\imath}+y\vec{\jmath}+z\vec{k}    \vec{u}(\vec{r})=u_x\vec{\imath}+u_y\vec{\jmath}+u_z\vec{k}

y al origen nos queda

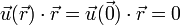
\vec{u}(\vec{r})\cdot\vec{r}=\vec{u}(\vec{0})\cdot\vec{r}= 0

esto es, que la velocidad en cada punto es ortogonal al vector de posición de dicho punto.

Si ahora aplicamos la condición al mismo punto 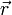\vec{r} y al punto 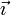\vec{\imath} tenemos

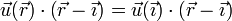
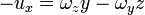
\vec{u}(\vec{r})\cdot\left(\vec{r}-\vec{\imath}\right)=\vec{u}(\vec{\imath})\cdot\left(\vec{r}-\vec{\imath}\right)   \Rightarrow    -u_x=\omega_zy-\omega_yz\,

y aplicándolo al mismo punto con los otros vectores de la base

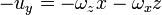
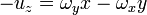
-u_y=-\omega_zx-\omega_xz\,    -u_z=\omega_yx-\omega_xy\,

esto es

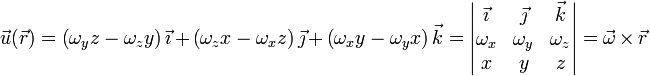
\vec{u}(\vec{r}) = \left(\omega_yz-\omega_zy\right)\vec{\imath}+\left(\omega_zx-\omega_xz\right)\vec{\jmath}+\left(\omega_xy-\omega_yx\right)\vec{k}=\left|\begin{matrix}\vec{\imath} & \vec{\jmath} & \vec{k} \\ \omega_x & \omega_y & \omega_z \\ x & y & z\end{matrix}\right|=\vec{\omega}\times\vec{r}

y volviendo a nuestro campo de velocidades original, 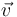\vec{v}

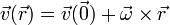
\vec{v}(\vec{r})=\vec{v}(\vec{0}) +\vec{\omega}\times\vec{r}

con lo que se completa la demostración del teorema de Chasles.

Obtenido de "http://tesla.us.es/wiki/index.php/Teorema_de_Chasles"

Herramientas:

Herramientas personales
TOOLBOX
LANGUAGES
licencia de Creative Commons
 Aviso legal - Acerca de Laplace