Vectores libres
De Laplace
(→Bases vectoriales. Componentes de un vector. Coordenadas de un punto) |
(→Bases vectoriales. Componentes de un vector. Coordenadas de un punto) |
||
| Línea 161: | Línea 161: | ||
Todas las bases de un espacio vectorial poseen el mismo número de vectores. Este número es la ''dimensión del espacio'' que, en el espacio ordinario es 3. | Todas las bases de un espacio vectorial poseen el mismo número de vectores. Este número es la ''dimensión del espacio'' que, en el espacio ordinario es 3. | ||
| - | == | + | ==Componentes de un vector. Coordenadas de un punto== |
Una '''base''' de vectores libres en el espacio ordinario tridimensional <math>E_3</math> es cualquier terna de vectores, <math>B=\{\vec{v}_1,\vec{v}_2,\vec{v}_3\}</math>, tal que todo vector libre, <math>\vec{a}</math>, se pueda expresar como combinación lineal de ellos, es decir: | Una '''base''' de vectores libres en el espacio ordinario tridimensional <math>E_3</math> es cualquier terna de vectores, <math>B=\{\vec{v}_1,\vec{v}_2,\vec{v}_3\}</math>, tal que todo vector libre, <math>\vec{a}</math>, se pueda expresar como combinación lineal de ellos, es decir: | ||
Revisión de 20:14 19 jul 2010
Contenido |
1 Tipos de magnitudes
Una magnitud física es cualquier propiedad física susceptible de ser medida. Ejemplos: el tiempo (t), la velocidad
(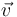 ), la masa (m), la temperatura (T), el campo eléctrico (
), la masa (m), la temperatura (T), el campo eléctrico (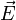 ).
).
Las magnitudes físicas se pueden clasificar en:
1.1 Magnitudes escalares
Las magnitudes escalares son aquéllas que quedan completamente determinadas mediante el conocimiento de su valor expresado mediante una cantidad (un número real) seguida de una unidad (a excepción de las adimensionales).
Ejemplos de magnitudes escalares son
- Tiempo (t)
- Masa (m)
- Temperatura (T)
- Carga eléctrica (q)
- …
1.2 Magnitudes vectoriales
Las magnitudes vectoriales son aquéllas que no quedan completamente determinadas por su valor (cantidad y unidad), sino que requieren además el conocimiento de la dirección y el sentido de su actuación y su punto de aplicación.
Entre las magnitudes vectoriales están:
- Velocidad (
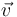 )
)
- Aceleración (
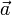 )
)
- Fuerza (
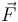 )
)
- Campo eléctrico (
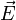 )
)
- …
Es importante tener siempre en mente la distinción entre cantidades escalares y vectoriales, ya que no pueden sumarse o igualarse cantidades de diferente tipo. Para señalar el carácter vectorial debe indicarse en la notación algún rasgo distintivo, normalmente una flecha sobre la cantidad. Así
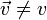
El primer símbolo, 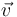 representa la velocidad, que posee módulo, dirección y sentido (no solo nos informa de cómo de rápido se mueve una partícula sino también hacia dónde se mueve). El segundo símbolo es el módulo de la velocidad (conocido como celeridad o rapidez) que no nos informa de la dirección de movimiento.
representa la velocidad, que posee módulo, dirección y sentido (no solo nos informa de cómo de rápido se mueve una partícula sino también hacia dónde se mueve). El segundo símbolo es el módulo de la velocidad (conocido como celeridad o rapidez) que no nos informa de la dirección de movimiento.
1.3 Otros tipos de magnitudes
Además de las magnitudes escalares y vectoriales, existen otros tipos de magnitudes “de orden superior”, conocidas en general como magnitudes tensoriales.
Una magnitud escalar se puede representar por un número 8con unidades), lo que equivale a una matriz 1×1. Una magnitud vectorial puede ser representadas por una vector fila o uno columna, que equivale a una matriz 1×3 o 3×1. Una magnitud tensorial requiere matrices 3×3 o incluso entes de mayores dimensiones.
Un ejemplo de magnitud tensorial son los “esfuerzos” en un sólido. Cuando se aplica una fuerza en una dirección resulta una deformación que puede ir en una dirección diferente. Por tanto necesitamos tanto la información de la dirección y sentido de los dos, fuerza y deformación, por lo que no nos basta con una magnitud vectorial.
En este curso las magnitudes tensoriales aparecen muy raramente.
1.4 Principio de homogeneidad
Una propiedad importante de las leyes físicas es que son homogéneas. Esto quiere decir que los dos miembros de una igualdad deben ser del mismo tipo:
- Una cantidad escalar será igual a otra cantidad escalar, por ejemplo
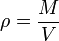
- Una cantidad vectorial será igual a otra cantidad vectorial
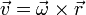
- pero nunca una cantidad escalar será igual a una vectorial. Por ejemplo, el momento de una fuerza es una cantidad cuyas unidades SI es 1 N·m, y la energía cinética es una magnitud cuya unidad es 1 J = 1 N·m, pero aunque se miden en las mismas unidades, el momento de una fuerza nunca puede ser igual a la energía cinética, pues la primera es una magnitud vectorial y la segunda es una escalar
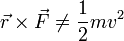
La energía cinética sí podrá ser igual al módulo del momento de la fuerza, que es una cantidad escalar
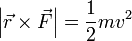
2 Vectores. Definición y clasificación
2.1 Definición
El concepto de vector es un concepto matemático con interés físico, ya que permite representar o describir las magnitudes vectoriales, así como operar con ellas.
Un vector geométrico es un segmento orientado dotado de los siguientes elementos:
- Módulo
- es su longitud, proporcional al valor de la magnitud física.
- Dirección
- Sentido
- es la orientación del segmento, indicada mediante una flecha y que permite definir cuál es su origen y cuál su extremo
- Punto de aplicación
- es el origen del segmento.
- Recta soporte
- es la recta a la que pertenece el segmento, definida mediante el punto de aplicación y la dirección marcada por el vector.
2.2 Tipos de vectores
Los vectores pueden clasificarse atendiendo a la cantidad de información que necesitamos para especificarlos.
2.2.1 Vectores ligados
Los vectores ligados constituyen el tipo básico. Para especificar un vector ligado necesitamos dar su módulo, su dirección y sentido y el punto de aplicación.
Un ejemplo de vector ligado lo constituye el campo eléctrico, que asigna a cada punto del espacio un vector 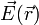 .
.
También es un vector ligado la velocidad, ya que va asociada a la posición instantánea que ocupa la partícula en movimiento.
2.2.2 Vectores deslizantes
El punto de aplicación de un vector ligado y la dirección del vector definen una recta, conocida como recta soporte.
Existen magnitudes físicas que aunque descritas en principio por vectores ligados, producen los mismos efectos si como punto de aplicación se toma cualquier otro situado en la misma recta soporte.
Un ejemplo de este tipo de vectores lo constituyen las fuerzas sobre un sólido. Es indiferente empujar un sólido por detrás o tirar de él desde delante, siempre que la recta soporte sea la misma.
Los vectores que cumplen esta propiedad se denominan vectores deslizantes (ya que pueden deslizarse libremente a lo largo de su recta soporte). Para especificar un vector deslizante, además del módulo, dirección y sentido, debe indicarse la recta soporte sobre la que se encuentra, pero no es necesario precisar un punto concreto de aplicación.
2.2.3 Vectores libres
Existen magnitudes físicas cuya descripción no requiere precisar un punto de aplicación, ni siquiera una recta soporte, pues para cualquier punto de aplicación en todo el espacio, sus consecuencias físicas son las mismas.
Un ejemplo lo tenemos en la resultante de todas las fuerzas que actúan sobre un sólido rígido.
En principio, cada magnitud física vectorial, según su naturaleza, puede ser representada por una de estas tres clases de vectores. Sin embargo, en ocasiones, es la naturaleza del problema físico concreto la que determina que una misma magnitud se describa mediante una u otra clase de vectores. Así, por ejemplo, una fuerza se comporta como un vector deslizante cuando actúa sobre un sólido rígido, y como un vector ligado cuando lo hace sobre un sólido deformable.
3 Suma de vectores
Los vectores libres forman parte de un espacio vectorial, por lo que admiten la definición de las operaciones suma y producto por un escalar con una serie de propiedades algebraicas (definición algebraica de vector).
La suma de vectores libres,
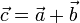
se define gráficamente de dos formas equivalentes:
- Colocándolos con el mismo origen: la suma vectorial será la diagonal del paralelogramo que definen (regla del paralelogramo).
- Colocando uno a continuación del otro y uniendo el origen del primero con el extremo del segundo (regla del triángulo).
Nótese que ambas definiciones requieren que los vectores sean libres, para que sus orígenes puedan trasladarse sin restricción.
Esta suma así definida presenta las siguientes propiedades algebraicas:
- Conmutativa
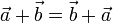
- Asociativa
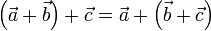
- Existencia de elemento neutro
- Existe un vector de módulo nulo,
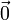 , tal que
, tal que
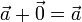
- Existencia de elemento opuesto
- Para cada vector no nulo,
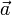 existe uno como el mismo módulo y dirección y sentido opuesto,
existe uno como el mismo módulo y dirección y sentido opuesto, 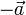 , tal que
, tal que
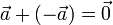
La operación suma, junto a la existencia de elemento opuesto, permite definir la resta o diferencia de vectores:
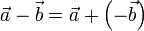
La propiedad asociativa, junto con la regla del triángulo, permite sumar n vectores a base de formar una línea quebrada disponiendo los vectores en sucesión y uniendo el origen del primero con el extremo del último.
4 Producto por un escalar
El producto de un vector libre, 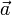 , por un escalar, λ (número real), se define como un nuevo vector libre,
, por un escalar, λ (número real), se define como un nuevo vector libre, 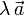 , cuyo módulo es igual al producto del escalar (en valor absoluto) por el módulo del vector original, cuya dirección es la misma que la del vector original, y cuyo sentido es el mismo o el opuesto al del vector original según el escalar sea positivo o negativo, respectivamente. Esta operación presenta las siguientes propiedades algebraicas:
, cuyo módulo es igual al producto del escalar (en valor absoluto) por el módulo del vector original, cuya dirección es la misma que la del vector original, y cuyo sentido es el mismo o el opuesto al del vector original según el escalar sea positivo o negativo, respectivamente. Esta operación presenta las siguientes propiedades algebraicas:
- Asociativa respecto al producto por escalar
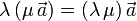
- Distributiva respecto a la suma de vectores
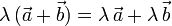
- Distributiva respecto a la suma de escalares
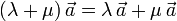
- Existencia de escalar unidad
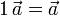
Combinando estas propiedades con las de la suma obtenemos, entre otras propiedades
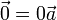
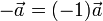
5 Vectores unitarios
Una vez definido el producto por un escalar, podomes obtener el vector unitario (de módulo unidad) en la dirección dada por un vector 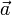 como el vector
como el vector

6 Combinaciones lineales
Uniendo las propiedades de la suma y el producto vectorial, podemos definir una combinación lineal de n vectores mediante la expresión
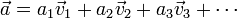
En este caso se dice que el vector 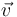 es linealmente dependiente de los vectores
es linealmente dependiente de los vectores 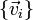 . Si no existe tal combinación lineal para obtener el vector
. Si no existe tal combinación lineal para obtener el vector 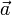 se dice que éste es linealmente independiente del conjunto.
se dice que éste es linealmente independiente del conjunto.
Un conjunto de vectores que permiten obtener todos los demás mediante combinaciones lineales se denomina sistema generador del espacio.
Un sistema generador cuyos vectores componentes son todos linealmente independientes entre sí (ninguno se puede poner como combinación lineal del resto) se denomina una base.
Todas las bases de un espacio vectorial poseen el mismo número de vectores. Este número es la dimensión del espacio que, en el espacio ordinario es 3.
7 Componentes de un vector. Coordenadas de un punto
Una base de vectores libres en el espacio ordinario tridimensional E3 es cualquier terna de vectores, 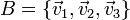 , tal que todo vector libre,
, tal que todo vector libre, 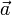 , se pueda expresar como combinación lineal de ellos, es decir:
, se pueda expresar como combinación lineal de ellos, es decir:
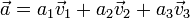
Se dice entonces que [a1,a2,a3] son las componentes del vector 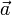 en la base vectorial B.
en la base vectorial B.
Por tanto, un mismo vector tendrá una terna distinta de componentes en cada una de las infinitas bases posibles. Por ello, es importante recordar siempre qué base se está empleando para expresar dicho vector. Una forma de garantizar que esto siempre esté presente es, para todo vector, usar la expresión como combinación lineal de la base dada más arriba.
Para describir el espacio ordinario, se puede definir un sistema de ejes coordenados cartesianos, OX1X2X3, al cual se le
asocia una base cartesiana ortonormal, 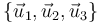 (formada por tres vectores unitarios, perpendiculares entre sí, que siguen las direcciones de los ejes OX1, OX2 y OX3, respectivamente). Cuando el sistema de ejes cartesianos es OXYZ, se prefiere la notación
(formada por tres vectores unitarios, perpendiculares entre sí, que siguen las direcciones de los ejes OX1, OX2 y OX3, respectivamente). Cuando el sistema de ejes cartesianos es OXYZ, se prefiere la notación 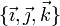 para su base ortonormal asociada.
para su base ortonormal asociada.
La posición de un punto genérico, P, respecto a un sistema de ejes cartesianos, OX1X2X3, queda unívocamente definida mediante su vector de posición:
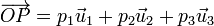
Se denominan coordenadas cartesianas del punto P en dicho sistema de ejes a las componentes de su vector de posición en la base ortonormal asociada, es decir, a la terna [p1,p2,p3].
Conocidas las coordenadas cartesianas del origen y del extremo de un vector, basta restarle las primeras a las segundas para obtener las
componentes cartesianas del vector. Por ejemplo, dados los puntos P(p1,p2,p3) y Q(q1,q2,q3), es inmediato calcular las componentes del vector 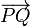 :
:
![\overrightarrow{PQ}=\overrightarrow{OQ}-\overrightarrow{OP}= [q_1-p_1,q_2-p_2,q_3-p_3]](/wiki/images/math/4/0/2/4024e5bfb4e949d06edeca0e8c713323.png)
8 Producto escalar
Dados dos vectores, 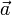 y
y  , que forman un ángulo θ (
, que forman un ángulo θ (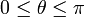 ), se denomina productoescalar,
), se denomina productoescalar, 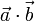 , al escalar (número real) que resulta de multiplicar los módulos de ambos vectores por el coseno del ángulo que forman:
, al escalar (número real) que resulta de multiplicar los módulos de ambos vectores por el coseno del ángulo que forman:
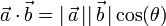
El producto escalar presenta las siguientes propiedades geométricas:
- Condición de ortogonalidad: si
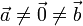 entonces
entonces 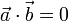

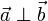
- Proyecciones ortogonales:
![\vec{a}\cdot\vec{b}=|\,\vec{a}\,|\;\mbox{proy}_{\parallel\vec{a}}\,[\,\vec{b}\,]= |\,\vec{b}\,|\;\mbox{proy}_{\parallel\vec{b}}\,[\,\vec{a}\,]](/wiki/images/math/2/f/e/2fee7fc2f1e9d6fb197964401807fa3f.png)
Aplicaciones:
- si
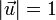 , entonces
, entonces ![\vec{a}\cdot\vec{u}=\mbox{proy}_{\parallel\vec{u}}\,[\,\vec{a}\,]\,](/wiki/images/math/6/d/0/6d00c65b125450daeb0a2763949361be.png)
- si
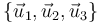 es ortonormal,
es ortonormal,
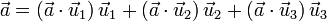
- Métrica (permite medir distancias y ángulos):
- Módulo de un vector
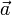 :
:
- Módulo de un vector
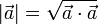
- Distancia entre dos puntos P y Q:
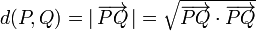
- Ángulo formado por dos rectas, r y s:
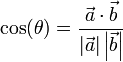
- Cosenos directores de una recta r:
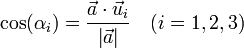
El producto escalar presenta las siguientes propiedades algebraicas:
- Asociativa respecto al producto por un escalar
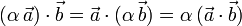
- Conmutativa
- Distributiva respecto a la suma
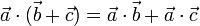
- Cancelativa
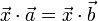

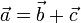 siendo
siendo 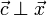 y, por tanto,
y, por tanto, 
Respecto al producto escalar en componentes cartesianas, destacaremos:
- Producto escalar de los vectores de una base cartesiana ortonormal,
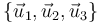 :
:
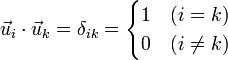
donde a δik se la denomina delta de kronecker
- Producto escalar de dos vectores arbitrarios,
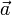 y
y  (se deduce del punto anterior y de las propiedades algebraicas):
(se deduce del punto anterior y de las propiedades algebraicas):
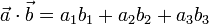
Aplicaciones:
- Módulo de un vector

- Distancia entre dos puntos
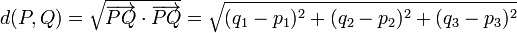
- Cosenos directores
![\cos(\alpha_i)=\frac{\vec{a}\cdot\vec{u}_i}{|\,\vec{a}\,|}= \frac{a_i}{[\,a_1^2+a_2^2+a_3^2\,]^{1/2}} \ (i=1,2,3)](/wiki/images/math/7/4/a/74a0dff6d528ffd680ed0eabd822e164.png) (obsérvese que: cos2(α1) + cos2(α2) + cos2(α3) = 1)
(obsérvese que: cos2(α1) + cos2(α2) + cos2(α3) = 1)
Finalmente, como aplicación geométrica del producto escalar, se puede deducir la ecuación vectorial normal del plano, π, que pasa por el punto P1(x1,y1,z1) y que es normal al vector ![\overrightarrow{N}=[\,\alpha,\beta,\gamma\,]](/wiki/images/math/a/6/d/a6de0f6129f701f2463130235d881148.png) . Si P(x,y,z) es un punto genérico del plano π, entonces:
. Si P(x,y,z) es un punto genérico del plano π, entonces:




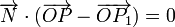

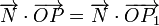
que, efectuando el producto escalar en componentes cartesianas, se traduce en que todo punto P(x,y,z) que pertenezca al plano π debe satisfacer la ecuación general:





