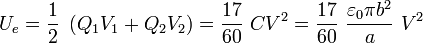Un disco y dos semidiscos paralelos

De Laplace

(Diferencias entre revisiones)

Revisión de 09:33 14 jul 2010

Contenido

1 Enunciado
2 Capacidades eléctricas de los condensadores
3 Circuito equivalente y matriz de coeficientes de capacidad
- 3.1 Obtención del circuito equivalente
- 3.2 Matriz de coeficientes de capacidad
4 Carga eléctrica y potencial para una configuración particular
5 Energía electrostática para dicha configuración

1 Enunciado

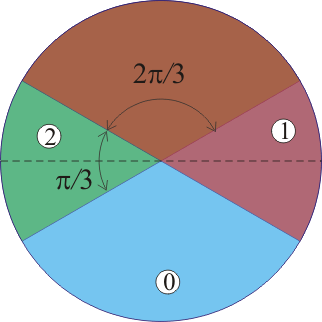
Un disco y un semidisco, ambos conductores y de igual radio b –que denominaremos conductores “0” y “1”, respectivamente– se hallan en sendos planos paralelos separados una distancia a. Un segundo semidisco –conductor “2”–, también de radio b se encuentra entre los conductores anteriores, a igual distancia a/2 de éstos. Los semidiscos no están alineados, sino que sus diámetros forman un ángulo α=60º (véase la figura). Las dimensiones son tales que b es mucho mayor que a de manera que, cuando el sistema se carga eléctricamente, las superficies conductoras enfrentadas pueden considerarse en influencia total, despreciándose los efectos de borde.

Teniendo en cuenta esta aproximación, determine las capacidades eléctricas de los distintos condensadores que forman el sistema de conductores descrito.
Tomando el disco completo como conductor de referencia (siempre conectado a tierra), obtenga el circuito equivalente y calcule la matriz de coeficientes de capacidad e inducción eléctrica del sistema.
Con el conductor “0” conectado a tierra y el “2” descargado y aislado, se conecta el conductor “1” a una fuente de potencial V. Calcule la carga eléctrica en el conductor “1” y el potencial en el conductor “2”.
Halle la energía electrostática del sistema en la configuración anterior.

2 Capacidades eléctricas de los condensadores

Supongamos que el disco y los semidiscos conductores almacenan sendos valores de carga eléctrica Q ₀, Q ₁ y Q ₂, hallándose en equilibrio electrostático. Cada conductor constituirá una superficie equiescalar para el potencial electrostático 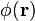$\ \phi (\mathbf{r})$ , que presentará valores V₀, V₁ y V₂, medidos respecto del origen de potencial que consideraremos situado en el infinito. En general, estos valores van a ser distintos de manera que entre cada par de conductores, así como entre cada uno de ellos y el infinito, hay una diferencia de potencial que se traduce en la existencia de un gradiente y, por tanto, de un campo eléctrico.

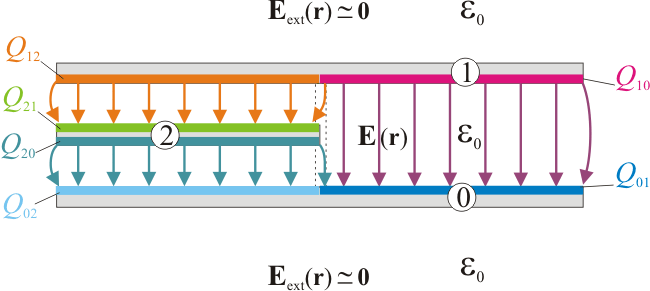
En el enunciado se indica que la distancia de separación a entre disco y semidisco exterior (conductores “0” y “1”, respectivamente) es mucho menor que el tamaño de los conductores (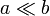 $a\ll b$ ). Esto permite realizar en el modelo una serie de simplificaciones que llevan a la obtención de una solución analítica sencilla para el problema del potencial. Como es bien sabido, ésta no va a ser la solución exacta, aunque los valores que proporciona para las diferentes magnitudes eléctricas pueden considerarse suficientemente precisos. En primer lugar se tendrá que el gradiente del potencial, 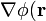$\nabla \phi (\mathbf{r}$ , en la región del espacio comprendida entre los conductores y el infinito va a tener un valor despreciable frente al que presentará en los puntos que se hallan entre los conductores; es decir, cuando éstos se hallan cargados eléctricamente y en equilibrio electrostático, el campo eléctrico en el exterior del sistema es prácticamente nulo si se compara con el que hay entre los conductores, pues 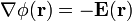$\nabla \phi (\mathbf{r})=-\mathbf{E}(\mathbf{r})$ . En consecuencia, la carga eléctrica en los conductores “1” y “0” se distribuirá exclusivamente en sus caras interiores, mientras que en el “2” lo hará en ambas caras, pues cada una de ellas se encuentra enfrentada a otro conductor del sistema. De esta forma, podemos expresar la cantidad de carga eléctrica en cada conductor de la siguiente manera:

$\begin{array}{c}Q_0=Q_{01}+Q_{02}\ \\ \\ Q_1=Q_{10}+Q_{12}\\ \\ Q_2=Q_{20}+Q_{21}\end{array}$

donde Q _ij es la cantidad parcial de carga eléctrica distribuida en el sector del conductor “i” que se encuentra directamente enfrentada al conductor “j”. Y también como consecuencia de la condición 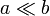$a\ll b$ , podemos considerar que los sectores enfrentados de cada par de conductores están en influencia total, almacenando cantidades opuestas de carga eléctrica y formando sendos condensadores de placas plano paralelas, caracterizados cada uno de ellos por su correspondiente capacidad eléctrica, C_pp^ij, que establece la relación entre la carga almacenada y la diferencia de potencial entre las placas:

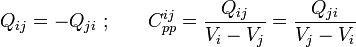
$Q_{ij}=-Q_{ji}\ \mathrm{;}\qquad C_{pp}^{ij}=\frac{Q_{ij}}{V_i-V_j}=\frac{Q_{ji}}{V_j-V_i}$

Como sabemos, la capacidad eléctrica es una magnitud que depende de la geometría del condensador. En el caso que estamos analizando, la proximidad entre las láminas conductoras en relación con su tamaño permite despreciar los efectos de borde, de manera que el campo eléctrico entre cada par de placas va a ser perpendicular a éstas y de módulo constante en prácticamente todos los puntos situados entre ellas. En consecuencia, la cantidad parcial de carga eléctrica Q _ij se distribuirá uniformemente en el sector del conductor “i” enfrentado al “j” y el correspondiente valor de capacidad se corresponderá con el del modelo ideal de condensador de placas plano paralelas,

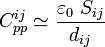
$C_{pp}^{ij}\simeq\frac{\varepsilon_0\ S_{ij}}{d_{ij}}$

siendo S_ij el área de los sectores en los conductores “i” y “j” que se encuentran en influencia total, y d_ij la distancia que los separa.

En el sistema bajo estudio los conductores “0” y “2” tienen enfrentados el sector correspondiente a un semidisco de radio b y están separados una distancia a/2:

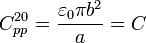
$S_{20}=\frac{\pi b^2}{2}\ \mathrm{;}\quad d_{20}=\frac{a}{2}\quad\Longrightarrow$ $C_{pp}^{20}=\frac{\varepsilon_0\pi b^2}{a}=C$

Los semidiscos conductores “1” y “2” están separados esa misma distancia y se encuentran girados un ángulo π/3, por lo que se enfrentan en un sector circular correspondiente a 2/3 de un semidisco (ó 1/3 de disco); se tendrá, por tanto,

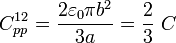
$S_{12}=\frac{\pi b^2}{3}\ \mathrm{;}\quad d_{12}=\frac{a}{2}\quad\Longrightarrow$ $C_{pp}^{12}=\frac{2 \varepsilon_0\pi b^2}{3 a}=\frac{2}{3}\ C$

Finalmente, los conductores “1” y “0” se enfrentan en un sector circular correspondiente a 1/3 de semidisco de radio b (o lo que es lo mismo, 1/6 de disco), separados una distancia a; entonces,

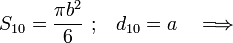
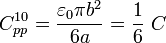
$S_{10}=\frac{\pi b^2}{6}\ \mathrm{;}\quad d_{10}=a\quad\Longrightarrow$ $C_{pp}^{10}=\frac{\varepsilon_0\pi b^2}{6 a}=\frac{1}{6}\ C$

3 Circuito equivalente y matriz de coeficientes de capacidad

Consideramos ahora el disco conductor “0” conectado a tierra, proporcionando así la referencia para los valores del potencial; es decir, V₀=0 y V₁, V₂, son los valores del potencial en los semidiscos “1” y “2” respecto del disco “0”.

3.1 Obtención del circuito equivalente

Para construir el circuito equivalente a un sistema electrostático colocamos un nodo por cada conductor (incluido el de referencia), y capacidades eléctricas para modelar cada tubo de líneas de campo eléctrico que partiendo de una superficie conductora terminan en otra. Estos tubos de campo determinan regiones conductoras (que pueden coincidir con la superficie completa o con parte de ella) en influencia total. En el caso de tubos de líneas de campo que empiezan o terminan en el conductor de refencia, la correspondiente capacidad del modelo se denomina autocapacidad.

Sea Q _ij la cantidad de carga en la región del conductor “i” que se encuentra en influencia total con todo o parte del “j”, y sea Q _i0 la que se encuentra en la parte de aquél conductor cuyas líneas llegan o vienen del conductor de referencia “0”. Las capacidades y autocapacidades del circuito equivalente se definen como,

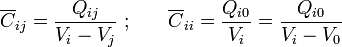
$\overline{C}_{ij}=\frac{Q_{ij}}{V_i-V_j}\ \mathrm{;}\qquad\overline{C}_{ii}=\frac{Q_{i0}}{V_i}=\frac{Q_{i0}}{V_i-V_0}$

El sistema bajo estudio está formado por tres conductores, incluyendo el disco conductor de referencia “0” y, según vimos en el apartado anterior, habrá líneas de campo eléctrico entre todos ellos. Por tanto, el circuito equivalente tendrá un condensador entre cada par de nodos. Además, obsérvese que las definiciones anteriores son idénticas a las de las capacidades de los condensadores plano-paralelos, cuyos valores de capacidad eléctrica fueron calculadas en el apartado anterior, en función de las propiedades geométricas. Teniendo en cuenta que el disco “0” es el conductor de referencia, se obtiene

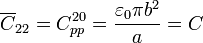
$\overline{C}_{22}=C_{pp}^{20}=\frac{\varepsilon_0\pi b^2}{a}=C$

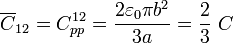
$\overline{C}_{12}=C_{pp}^{12}=\frac{2 \varepsilon_0\pi b^2}{3 a}=\frac{2}{3}\ C$

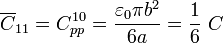
$\overline{C}_{11}=C_{pp}^{10}=\frac{\varepsilon_0\pi b^2}{6 a}=\frac{1}{6}\ C$

3.2 Matriz de coeficientes de capacidad

Esta matriz describe la carga eléctrica total en cada conductor como una combinación lineal de los potenciales en todos los conductores, medidos respecto del conductor de referencial. En nuestro caso de un sistema con 3 conductores (incluido el de referencia)es una matriz 2×2,

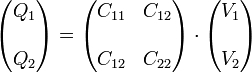
$\mathsf{C}=\begin{pmatrix}C_{11} & C_{12} \\ & \\ C_{12}& C_{22} \end{pmatrix}\$ , tal que $\quad\begin{pmatrix}Q_1 \\ \\ Q_2\end{pmatrix}=\begin{pmatrix}C_{11} & C_{12} \\ & \\ C_{12}& C_{22}\end{pmatrix}\cdot\begin{pmatrix}V_1 \\ \\ V_2\end{pmatrix}\quad$

Los valores de los coeficientes C_ij se obtienen fácilamene sin más que tener en cuenta su relación con las capacidades del circuito equivalente:

$C_{ii}=\sum_j\overline{C}_{ij}\quad\Longrightarrow\quad \begin{cases}\displaystyle C_{11}=\overline{C}_{11}+\overline{C}_{12}=\frac{1}{6}\ C+\frac{2}{3}\ C=\frac{5}{6}\ \frac{\varepsilon_0\pi b^2}{a}\\ \\ \displaystyle C_{22}=\overline{C}_{12}+\overline{C}_{22}=\frac{2}{3}\ C+ C=\frac{5}{3}\ \frac{\varepsilon_0\pi b^2}{a} \end{cases}$

$C_{ij}=-\overline{C}_{ij}\quad\Longrightarrow\quad C_{12}=-\overline{C}_{12}=-\frac{2}{3}\ C=-\frac{2}{3}\ \frac{\varepsilon_0\pi b^2}{a}$

Por tanto, la matriz de coeficientes será...

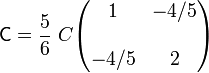$\mathsf{C}=\frac{5}{6}\ C\begin{pmatrix}1 & -4/5 \\ & \\ -4/5& 2 \end{pmatrix}$ con $C=\frac{\varepsilon_0\pi b^2}{a}$

4 Carga eléctrica y potencial para una configuración particular

Con el conductor “0” como referencia del potencial, conectamos el conductor “1” a una fuente de potencial de valor dado V, mientras que el semidisco interior “2” permanece descargado:

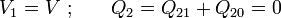
$V_1=V\ \mathrm{;}\qquad Q_2=Q_{21}+Q_{20}=0$

Para determinar la carga en el semidisco “1” y el potencial a que se encuentra el conductor “2” no hay más que exigir las relaciones que deben verificar los potenciales y las cargas en el sistema:

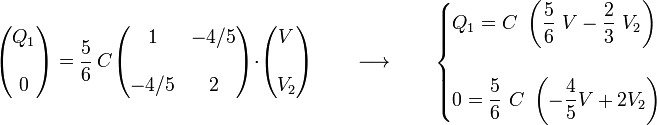
$\begin{pmatrix}Q_1 \\ \\ 0\end{pmatrix}=\frac{5}{6}\ C\begin{pmatrix}1 & -4/5 \\ & \\ -4/5& 2 \end{pmatrix}\cdot\begin{pmatrix}V \\ \\ V_2\end{pmatrix}\qquad\longrightarrow\qquad\begin{cases}\displaystyle Q_1= C \ \left(\frac{5}{6}\ V - \frac{2}{3}\ V_2\right) \\ \\ \displaystyle 0= \frac{5}{6}\ C \ \left(-\frac{4}{5} V + 2 V_2\right)\end{cases}$

Resolviendo este sistema de ecuaciones se obtiene

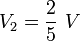
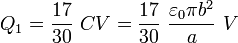
$V_2=\frac{2}{5}\ V$ $Q_1=\frac{17}{30}\ C V=\frac{17}{30}\ \frac{\varepsilon_0\pi b^2}{a}\ V$

5 Energía electrostática para dicha configuración

En un sistema electrostático formado por N+1 conductores, en general cargados eléctricamente, donde uno de ellos actúa como conductor de referencia, la energía electrostática almacenada por el sistema viene dada por la expresión,

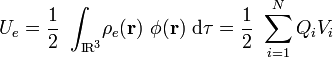
$U_e=\frac{1}{2}\ \int_{\mathrm{I}\!\mathrm{R}^3}\!\rho_e(\mathbf{r})\ \phi(\mathbf{r})\ \mathrm{d}\tau=\frac{1}{2}\ \sum_{i=1}^NQ_iV_i$

donde Q _“i” y V _“i” son, rspectivamente la carga del conductor “i” y el valor de su potencial medido respecto del conductor de referencia. En el caso de nuestro sistema de placas conductoras, en la configuración del apartado anterior se tendrá

$U_e=\frac{1}{2}\ \left(Q_1V_1+Q_2V_2\right)=\frac{17}{60}\ C V^2=\frac{17}{60}\ \frac{\varepsilon_0\pi b^2}{a}\ V^2$

@@ Línea 50: / Línea 50: @@
 [[Archivo:discoysemidiscos4.gif|left]]El sistema bajo estudio está formado por tres conductores, incluyendo el disco conductor de referencia &ldquo;0&rdquo; y, según vimos en el apartado anterior, habrá líneas de campo eléctrico entre todos ellos. Por tanto, el circuito equivalente tendrá un condensador entre cada par de nodos. Además, obsérvese que las definiciones anteriores son idénticas a las de las capacidades de los condensadores plano-paralelos, cuyos  valores de capacidad eléctrica fueron calculadas en el apartado anterior, en función de las propiedades geométricas. Teniendo en cuenta que el disco &ldquo;0&rdquo; es el conductor de referencia, se obtiene
+&nbsp;
 <center><math style="border:solid green 2px;padding:7px">\overline{C}_{22}=C_{pp}^{20}=\frac{\varepsilon_0\pi b^2}{a}=C</math></center>
 &nbsp;
 <center><math style="border:solid orange 2px;padding:7px">\overline{C}_{12}=C_{pp}^{12}=\frac{2 \varepsilon_0\pi b^2}{3 a}=\frac{2}{3}\ C</math></center>
+&nbsp;
 <center><math style="border:solid violet 2px;padding:7px">\overline{C}_{11}=C_{pp}^{10}=\frac{\varepsilon_0\pi b^2}{6 a}=\frac{1}{6}\ C</math></center>

Un disco y dos semidiscos paralelos

De Laplace

Revisión de 09:33 14 jul 2010

Contenido

1 Enunciado

2 Capacidades eléctricas de los condensadores

3 Circuito equivalente y matriz de coeficientes de capacidad

3.1 Obtención del circuito equivalente

3.2 Matriz de coeficientes de capacidad

4 Carga eléctrica y potencial para una configuración particular

5 Energía electrostática para dicha configuración

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES