Caso práctico de ciclo de Stirling

De Laplace

(Diferencias entre revisiones)

Revisión de 11:54 12 jul 2010

Contenido

1 Enunciado
2 Intercambios energéticos
- 2.1 Presiones, volúmenes y temperaturas
- 2.2 Trabajo, calor y energía interna
3 Variación de la entropía
4 Comparación de rendimientos
5 Modelo del ciclo

1 Enunciado

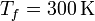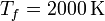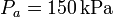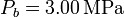100 moles de gas ideal diátomico sufre un ciclo de Stirling internamente reversible, representado en la figura. El ciclo se compone de dos isotermas y dos isócoras. Las temperaturas de trabajo son $T_f = 300\,\mathrm{K}$ y $T_f = 2000\,\mathrm{K}$ , mientras que las presiones extremas son $P_a = 150\,\mathrm{kPa}$ y $P_b = 3.00\,\mathrm{MPa}$ .

En cada uno de los procesos, calcula la variación de energía interna, el trabajo realizado y el calor absorbido por el gas. Calcula el rendimiento del ciclo.
Calcula la variación de entropía en cada proceso del ciclo y la variación neta en el ciclo completo.
Compara el rendimiento del ciclo con el de una máquina de Carnot reversible que trabaje entre las mismas temperaturas.
Imagina y describe un experimento que te permita recorrer el ciclo.

Dato: 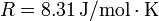$R = 8.31\,\mathrm{J}/\mathrm{mol}\cdot\mathrm{K}$

2 Intercambios energéticos

2.1 Presiones, volúmenes y temperaturas

Antes de calcular el trabajo y el calor en cada proceso, es conveniente conocer las presiones, volúmenes y temperaturas de los cuatro vértices del ciclo, puesto que necesitaremos estos valores en los cálculos posteriores.

Para ello, iremos rellenando progresivamente la tabla con $p$ , $V$ y $T$ para los estados 1, 2, 3 y 4.

Comenzamos escribiendo los datos del problema, que son la temperatura de los estados 1 y 2 (que están a la misma, $T f$ ), la de los estados 3 y 4 (que están a $T c$ ), la presión en el estado 1 (que es $p a$ ) y la presión en el 3 (que es $p b$ )

Estado	p (MPa)	T (K)
1	0.15	300
2		300
3	3.00	2000
4		2000

Ahora, para cada fila en la que conozcamos dos datos, podemos hallar el tercero despejando en la ecuación de estado de los gases ideales, dado que conocemos el número de moles de gas (n = 100 moles)

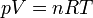
$pV = nRT\,$

Así, obtenemos el volumen inicial, del estado 1,

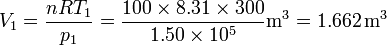
$V_1 = \frac{nRT_1}{p_1}=\frac{100\times 8.31\times 300}{1.50\times 10^5}\mathrm{m}^3 = 1.662\,\mathrm{m}^3$

Obsérvese que, puesto que estamos trabajando en el SI, el resultado está en metros cúbicos, que es la unidad SI de volumen.

Del mismo modo, hallamos el volumen en el estado 3

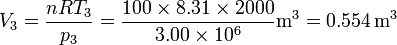
$V_3 = \frac{nRT_3}{p_3}=\frac{100\times 8.31\times 2000}{3.00\times 10^6}\mathrm{m}^3 = 0.554\,\mathrm{m}^3$

Incluimos estos dos datos en la tabla

Estado	p (MPa)	V (m³)	T (K)
1	0.15	1.662	300
2			300
3	3.00	0.554	2000
4			2000

Ahora, dado que los procesos 2→3 y 4→1 son isócoros, el volumen en el estado 2 es el mismo que en el 3, y el del 4 es el mismo que en el 1. Incluyendo estos dos datos:

Estado	p (MPa)	V (m³)	T (K)
1	0.15	1.662	300
2		0.554	300
3	3.00	0.554	2000
4		1.662	2000

Por último, hallamos la presión en los estados 3 y 4 empleando de nuevo la ecuación de los gases ideales

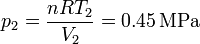
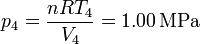
$p_2 = \frac{n R T_2}{V_2} = 0.45\,\mathrm{MPa}$ $p_4 = \frac{n R T_4}{V_4} = 1.00\,\mathrm{MPa}$

Con esto ya tenemos completa la tabla:

Estado	p (MPa)	V (m³)	T (K)
1	0.15	1.662	300
2	0.45	0.554	300
3	3.00	0.554	2000
4	1.00	1.662	2000

Alternativamente, podemos calcular la presión en los estados 2 y 4 aplicando que los procesos 2→3 y 4→1 son a volumen constante y por tanto

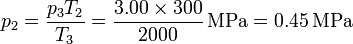
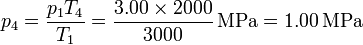
$p_2 = \frac{p_3T_2}{T_3}=\frac{3.00 \times 300}{2000}\,\mathrm{MPa} = 0.45\,\mathrm{MPa}$ $p_4 = \frac{p_1T_4}{T_1}=\frac{3.00 \times 2000}{3000}\,\mathrm{MPa} = 1.00\,\mathrm{MPa}$

Ahora procedemos al cálculo de los intercambios energéticos en cada paso.

2.2 Trabajo, calor y energía interna

2.2.1 Compresión isoterma 1→2

En el primer paso, tenemos que el volumen de gas se reduce sin variar su temperatura. Por tratarse de un gas ideal, la energía interna no cambia en este proceso

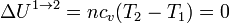
$\Delta U^{1\to 2} = nc_v(T_2-T_1) = 0\,$

El trabajo lo calculamos a partir de su expresión para un proceso isotermo reversible a temperatura $T f$

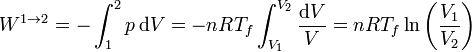
$W^{1\to 2} =-\int_1^2 p\,\mathrm{d}V = -nRT_f\int_{V_1}^{V_2} \frac{\mathrm{d}V}{V}=nRT_f\ln\left(\frac{V_1}{V_2}\right)$

Sustituyendo los valores numéricos

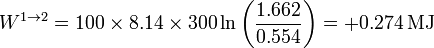
$W^{1\to 2} =100\times 8.14\times 300 \ln\left(\frac{1.662}{0.554}\right)=+0.274\,\mathrm{MJ}$

El calor en este proceso lo obtenemos a partir del primer principio de la termodinámica

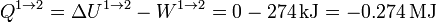
$Q^{1\to 2} = \Delta U^{1\to 2} - W^{1\to 2} = 0 - 274\,\mathrm{kJ} = -0.274\,\mathrm{MJ}$

2.2.2 Calentamiento isócoro 2→3

En el segundo proceso, por ser a volumen constante, el trabajo realizado sobre el gas es nulo

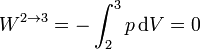
$W^{2\to 3}= -\int_2^3 p\,\mathrm{d}V = 0$

El calor en este proceso es el correspondiente a un proceso a volumen constante

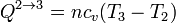
$Q^{2\to 3}= nc_v(T_3-T_2)$

Por tratarse de un gas diatómico la capacidad calorífica molar a volumen constante es

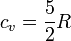
$c_v = \frac{5}{2}R$

y el valor numérico del calor es

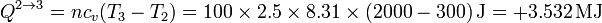
$Q^{2\to 3}= nc_v(T_3-T_2)= 100\times 2.5\times 8.31\times(2000-300)\,\mathrm{J} = +3.532\,\mathrm{MJ}$

La variación de la energía interna en este proceso coincide con el calor

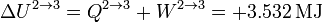
$\Delta U^{2\to 3} = Q^{2\to 3} + W^{2\to 3} = +3.532\,\mathrm{MJ}$

2.2.3 Expansión isoterma 3→4

Cuando el gas se expande a temperatura constante, la energía interna permanece constante

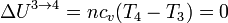
$\Delta U^{3\to 4} = nc_v(T_4-T_3) = 0$

y el trabajo es de nuevo el de un proceso isotermo, pero ahora a temperatura $T c$

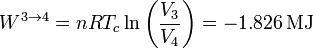
$W^{3\to 4} =nRT_c\ln\left(\frac{V_3}{V_4}\right) = -1.826\,\mathrm{MJ}$

Vemos que ahora el trabajo es negativo, pues es el sistema el que lo realiza sobre el ambiente.

El calor es igual a esta cantidad, con signo contrario

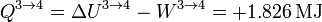
$Q^{3\to 4} = \Delta U^{3\to 4} - W^{3\to 4} = +1.826\,\mathrm{MJ}$

2.2.4 Enfriamiento isócoro 4→1

Por último, el gas se enfría manteniendo su volumen constante. El trabajo en este proceso es nulo

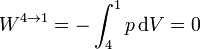
$W^{4\to 1}= -\int_4^1 p\,\mathrm{d}V = 0$

y el calor es el de un proceso a volumen constante

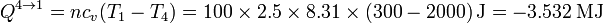
$Q^{4\to 1}= nc_v(T_1-T_4)= 100\times 2.5\times 8.31\times(300-2000)\,\mathrm{J} = -3.532\,\mathrm{MJ}$

Nótese que resulta el mismo que en el calentamiento, pero con el signo cambiado, por ser un descenso de temperatura exactamente opuesto al ascenso anterior.

La variación de energía coincide con el calor en este proceso

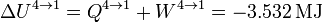
$\Delta U^{4\to 1} = Q^{4\to 1} + W^{4\to 1} = -3.532\,\mathrm{MJ}$

2.2.5 Cuadro resumen

En un ejercicio de contabilidad, podemos tabular todos los resultados y hallar el valor neto para cada magnitud

Proceso	W (MJ)	Q (MJ)	ΔU (MJ)
1→2	+0.274	−0.274	0
2→3	0	+3.532	+3.532
3→4	−1.826	+1.826	0
4→1	0	−3.532	−3.532
Total	−1.552	+1.552	0

El trabajo neto realizado sobre el sistema es negativo, como corresponde a una máquina térmica.

2.2.6 Rendimiento

El rendimiento de una máquina térmica es el cociente entre el valor absoluto del trabajo neto realizado por la máquina y el calor absorbido (no el calor neto). En este caso se absorbe calor tanto en el proceso 2→3 como en el 3→4, por lo que el rendimiento es

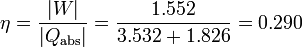
$\eta = \frac{|W|}{|Q_\mathrm{abs}|}=\frac{1.552}{3.532+1.826}= 0.290$

3 Variación de la entropía

Para la entropía tenemos de nuevo cuatro cálculos separados, uno por proceso:

3.1 Compresión isoterma 1→2

Este es un proceso reversible isotermo, por lo que la variación de entropía en él es simplemente

No se pudo entender (Falta el ejecutable de texvc. Por favor, lea math/README para configurarlo.): \Delta S^{1\to 2} = \frac{Q^{1\to 2}}{T_f} = -0.913\,\frac{\mathrm{kJ}}{\mathrm{K}

3.2 Calentamiento isócoro 2→3

El calentamiento no se produce a temperatura constante, obviamente, por lo que la variación de entropía no puede calcularse simplemente dividiendo el calor por una temperatura (¿cuál?). En su lugar es preciso hacer una integral, aprovechando que el proceso es internamente reversible

No se pudo entender (Falta el ejecutable de texvc. Por favor, lea math/README para configurarlo.): \Delta S^{2\to 3}=\int_2^3 \frac{\delta Q_r}{T} = n c_v\int_{T_2}^{T_3}\frac{\mathrm{d}T}{T}= nc_v\ln\left(\frac{T_3}{T_2}\right) = +3.941\,\frac{\mathrm{kJ}}{\mathrm{K}

3.3 Expansión isoterma 3→4

De nuevo tenemos un proceso reversible isotermo, con variación de entropía

No se pudo entender (Falta el ejecutable de texvc. Por favor, lea math/README para configurarlo.): \Delta S^{3\to 4} = \frac{Q^{3\to 4}}{T_c} = +0.913\,\frac{\mathrm{kJ}}{\mathrm{K}

3.4 Enfriamiento isócoro 4→1

En el último paso debemos integrar de nuevo

No se pudo entender (Falta el ejecutable de texvc. Por favor, lea math/README para configurarlo.): \Delta S^{4\to 1}= nc_v\ln\left(\frac{T_1}{T_4}\right) = -3.941\,\frac{\mathrm{kJ}}{\mathrm{K}

3.5 Variación neta de entropía

Sumando los cuatro incrementos obtenemos la variación neta de entropía en el sistema en un ciclo

No se pudo entender (Falta el ejecutable de texvc. Por favor, lea math/README para configurarlo.): \Delta S = \Delta S^{1\to 2} + \Delta S^{1\to 2} + \Delta S^{1\to 2} + \Delta S^{1\to 2} =(-0.913+3.941+0.913-3.941)\,\frac{\mathrm{kJ}}{\mathrm{K} = 0

Esta variación es nula como corresponde a una función de estado en un ciclo cerrado.

3.6 Entropía de un gas ideal

Las variaciones de entropía calculadas anteriormente pueden hallarse también usando la expresión general de la variación en la entropía de un gas ideal

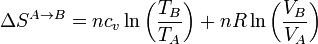
$\Delta S^{A\to B} = n c_v\ln\left(\frac{T_B}{T_A}\right)+n R \ln\left(\frac{V_B}{V_A}\right)$

En este ciclo de Stirling esta fórmula es especialmente sencilla de utilizar pues en cada paso se anula uno de los dos términos.

4 Comparación de rendimientos

El rendimiento máximo de una máquina térmica que opere entre las temperaturas T_f y T_c es el correspondiente a una máquina de Carnot

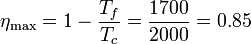
$\eta_\mathrm{max} = 1 - \frac{T_f}{T_c} = \frac{1700}{2000} = 0.85$

Vemos que es muy superior al obtenido en el primer apartado para este ciclo. El rendimiento relativo (o rendimiento del segundo principio) es

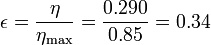
$\epsilon = \frac{\eta}{\eta_\mathrm{max}} = \frac{0.290}{0.85} = 0.34$

esto es, el rendimiento es solo un 34% del máximo ideal. Este rendimiento puede mejorarse en un motor de Stirling real introduciendo la recirculación del calor, de forma que no haga falta absorber tanto.

5 Modelo del ciclo

El modelo más sencillo para este ciclo consiste únicamente en un cilindro de paredes diatermas con un émbolo. El émbolo posee dos posiciones extremas, que pueden fijarse con pernos de forma que pueda mantenerse el volumen constante. El proceso sería el siguiente.

Compresión isoterma: Se sumerge el cilindro en un baño a temperatura T_f. Se aumenta

lentamente la presión externa sobre el émbolo de forma que el volumen se va reduciendo. A través de las paredes va escapando calor, de forma que la temperatura se mantiene constante.

Calentamiento isócoro: Se fija el pistón en su posición final con un perno, de forma que

el volumen permanece constante. Se va aumentando gradualmente la temperatura del baño térmico que envuelve al sistema, hasta alcanzar la temperatura final.

Expansión isoterma: El pistón está sometido a una gran diferencia de presiones entre el

gas interior y el exterior, por lo que si se retira el perno bruscamente, el pistón saldría disparado. Por ello, primero se aumenta la presión externa hasta igualarla con la interna. Acto seguido se retira el perno. Ahora se va reduciendo la presión externa, sin retirarlo del baño caliente, hasta que el volumen vuelva a ser el inicial. Finalmente, el pistón se fija con otro perno.

Enfriamiento isócoro: Se baja la temperatura del baño hasta volver a la temperatura

inicial. Para evitar una implosión del gas al retirar el perno, se reduce la presión externa hasta igualar a la inicial. El ciclo está completo.

@@ Línea 176: / Línea 176: @@
 ===Trabajo, calor y energía interna===
 ====Compresión isoterma 1&rarr;2====
-En el primer paso, tenemos que el volumen de gas se reduce sin variar su temperatura. Por
+En el primer paso, tenemos que el volumen de gas se reduce sin variar su temperatura. Por tratarse de un gas ideal, la energía interna no cambia en este proceso
-tratarse de un gas ideal, la energía interna no cambia en este proceso
-<center><math>\Delta U^{1\to 2} = nc_v(T_2-T_1) = 0</math></center>
+<center><math>\Delta U^{1\to 2} = nc_v(T_2-T_1) = 0\,</math></center>
-El trabajo lo calculamos a partir de su expresión para un proceso isotermo reversible a
+El trabajo lo calculamos a partir de su expresión para un proceso isotermo reversible a temperatura <math>T_f</math>
-temperatura <math>T_f</math>
 <center><math>W^{1\to 2} =-\int_1^2 p\,\mathrm{d}V = -nRT_f\int_{V_1}^{V_2}