Modelo de molécula de hidrógeno
De Laplace
(Diferencias entre revisiones)
(→Enunciado) |
|||
| Línea 10: | Línea 10: | ||
==Posición de equilibrio== | ==Posición de equilibrio== | ||
| + | Las cargas positivas se repelen mutuamente. Sin embargo no se alejan indefinidamente debido a la fuerza debida a la nube negativa, que las empuja hacia el centro y que es más intensa cuanto más se alejan del centro. | ||
| + | |||
| + | La condición de equilibrio para una de las cargas positivas es que la fuerza total sobre ella se anule | ||
| + | |||
| + | <center><math>\mathbf{F}_1=e\left(\mathbf{E}_q(\mathbf{r}_1)+\mathbf{E}_\rho(\mathbf{r}_1))=\mathbf{0}</math></center> | ||
| + | |||
| + | Si suponemos uno de los núcleos situado en <math>\mathbf{r}_1=z_0\mathbf{u}_z</math> y el otro en <math>\mathbf{r}_2=-z_0\mathbf{u}_z</math>, el campo que el segundo produce en la posición del primero es | ||
==Potencial y campo eléctrico== | ==Potencial y campo eléctrico== | ||
===Campo eléctrico=== | ===Campo eléctrico=== | ||
Revisión de 18:10 28 jun 2010
Contenido |
1 Enunciado
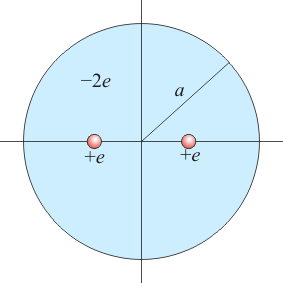
Un modelo simple de la molécula de hidrógeno es el siguiente: tenemos dos cargas puntuales (los núcleos) de valor + e inmersas en una nube esférica de radio a, con carga − 2e distribuida uniformemente.
- Determine la posición de equilibrio entre las dos cargas puntuales, suponiendo que se encuentran situadas simétricamente respecto al centro de la nube.
- Calcule el potencial y el campo eléctrico en todos los puntos del espacio en la situación anterior.
- Suponga que las dos cargas positivas se desplazan una cantidad c = a / 4 a lo largo de la recta que las une, manteniendo la distancia entre ellas. En este caso, ¿qué campo se ve en el exterior de la molécula? ¿cuáles son los dos primeros momentos del desarrollo multipolar del potencial eléctrico?
- Calcule el trabajo necesario para realizar el desplazamiento del apartado anterior.
2 Posición de equilibrio
Las cargas positivas se repelen mutuamente. Sin embargo no se alejan indefinidamente debido a la fuerza debida a la nube negativa, que las empuja hacia el centro y que es más intensa cuanto más se alejan del centro.
La condición de equilibrio para una de las cargas positivas es que la fuerza total sobre ella se anule
Si suponemos uno de los núcleos situado en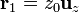 
y el otro en 
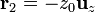, el campo que el segundo produce en la posición del primero es
