Espiral logarítmica
De Laplace
(Diferencias entre revisiones)
(→Ley horaria) |
(→Enunciado) |
||
| Línea 2: | Línea 2: | ||
Una partícula recorre la espiral logarítmica de ecuación | Una partícula recorre la espiral logarítmica de ecuación | ||
| - | <center><math>\vec{r} = | + | <center><math>\vec{r} = b (\cos(\theta)\vec{\imath}+\,\mathrm{sen}(\theta)\vec{\jmath})\mathrm{e}^{-\theta\,\mathrm{cotg}\,\alpha}</math></center> |
| - | donde <math> | + | donde <math>b</math> y <math>\alpha</math> son constantes. El movimiento es uniforme a lo largo de la curva, con celeridad constante <math>v_0</math>. En el instante inicial la partícula se encuentra en <math>\theta=0</math> |
# Determine la ley horaria <math>\theta = \theta(t)</math>. | # Determine la ley horaria <math>\theta = \theta(t)</math>. | ||
Revisión de 08:31 25 jun 2010
Contenido |
1 Enunciado
Una partícula recorre la espiral logarítmica de ecuación
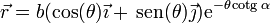
donde b y α son constantes. El movimiento es uniforme a lo largo de la curva, con celeridad constante v0. En el instante inicial la partícula se encuentra en θ = 0
- Determine la ley horaria θ = θ(t).
- Calcule el tiempo que tarda en llegar a
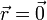. ¿Cuántas vueltas da para ello?
- Halle el vector aceleración y sus componentes intrínsecas en cada punto de la trayectoria.
- Determine la posición de los centros de curvatura de este movimiento.
2 Ley horaria
Para hallar la ley horaria θ = θ(t) aplicamos que el movimiento es uniforme y por tanto
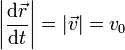
Sin embargo, lo que se nos da es la trayectoria como función de la coordenada θ y la velocidad no es la derivada de la posición respecto a θ, sino respecto al tiempo. Para relacionar las dos cosas aplicamos la regla de la cadena
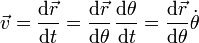
Aquí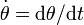 
es una función que debemos determinar.
Tomando módulos
