Espiral logarítmica
De Laplace
(Diferencias entre revisiones)
(→Enunciado) |
|||
| Línea 11: | Línea 11: | ||
# Determine la posición de los centros de curvatura de este movimiento. | # Determine la posición de los centros de curvatura de este movimiento. | ||
| + | ==Ley horaria== | ||
| + | Para hallar la ley horaria <math>\theta = \theta(t)</math> aplicamos | ||
| + | ==Tiempo en llegar al origen== | ||
| + | ==Aceleración== | ||
| + | ==Centros de curvatura== | ||
[[Categoría:Problemas de cinemática de la partícula]] | [[Categoría:Problemas de cinemática de la partícula]] | ||
Revisión de 21:07 24 jun 2010
Contenido |
1 Enunciado
Una partícula recorre la espiral logarítmica de ecuación
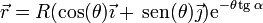
donde R y α son constantes. El movimiento es uniforme a lo largo de la curva, con celeridad constante v0. En el instante inicial la partícula se encuentra en θ = 0
- Determine la ley horaria θ = θ(t).
- Calcule el tiempo que tarda en llegar a
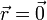. ¿Cuántas vueltas da para ello?
- Halle el vector aceleración y sus componentes intrínsecas en cada punto de la trayectoria.
- Determine la posición de los centros de curvatura de este movimiento.
2 Ley horaria
Para hallar la ley horaria θ = θ(t) aplicamos
