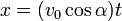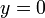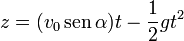|
|
| (178 ediciones intermedias no se muestran.) |
| Línea 1: |
Línea 1: |
| - | ==[[2.1. Ejemplo de movimiento plano en 3D|Ejemplo de movimiento plano en 3D]]==
| |
| - | Una partícula describe un movimiento según la ecuación horaria
| |
| - |
| |
| - | <center><math>\vec{r}(t) = 4A\cos^2(\omega t)\vec{\imath}+5A\cos(\omega t)\,\mathrm{sen}(\omega t)\vec{\jmath}-3A\cos^2(\omega t)\vec{k}</math></center>
| |
| - |
| |
| - | # Calcule la velocidad y la aceleración instantáneas de este movimiento.
| |
| - | # Determine el parámetro arco como función del tiempo y escriba la ecuación de la trayectoria como función del parámetro arco.
| |
| - | # Calcule el triedro de Frenet asociado a la trayectoria en cada instante, así como las componentes intrínsecas de la aceleración.
| |
| - | # Halle el radio de curvatura y la posición del centro de curvatura en cada instante. ¿Qué tipo de movimiento describe la partícula?
| |
| - |
| |
| - | ==[[2.2. Evolvente de una circunferencia|Evolvente de una circunferencia]]==
| |
| - | [[Archivo:problema-evolvente.png|right]]
| |
| - | La ''evolvente'' de una circunferencia es la curva plana que se obtiene cuando se desenrolla un hilo tenso de un carrete circular. Suponga que se tiene una bobina de radio <math>A</math> que se va desenrollando a ritmo constante, de forma que el punto <math>C</math> donde el hilo deja de hacer contacto con el carrete forma un ángulo <math>\theta=\omega t</math> con el eje <math>OX</math>. Una partícula material se
| |
| - | encuentra en el punto <math>P</math> situado en el extremo del hilo, moviéndose con este extremo a medida que el hilo se va desenrollando.
| |
| - |
| |
| - | # Determine el vector de posición de la partícula.
| |
| - | # Calcule la velocidad y la aceleración de la partícula.
| |
| - | # Determine la ley horaria <math>s=s(t)</math>.
| |
| - | # Halle los vectores tangente y normal a la trayectoria.
| |
| - | # Halle el radio de curvatura y el centro de curvatura.
| |
| - |
| |
| - | ==[[2.3. Movimiento de partícula sujeta de un hilo|Movimiento de partícula sujeta de un hilo]]==
| |
| - |
| |
| - | [[Archivo:particula-polea.png|right]]
| |
| - |
| |
| - | Una barra rígida <math>AB</math> de longitud <math>L</math> se mueve en un plano vertical <math>OXY</math>, manteniendo su extremo <math>A</math> articulado en un punto del eje horizontal de coordenadas <math>\overrightarrow{OA}= L \vec{\imath}</math>, y verificando la ley horaria <math>\theta(t) = 2\omega t</math>, con <math>0 \leq \theta \leq \pi</math> y siendo <math>\omega =</math> cte. Un hilo inextensible de longitud <math>2L</math> tiene uno de sus extremos conectado al origen del sistema de referencia (punto <math>O</math>), mientras que del otro cuelga una partícula <math>P</math> que mantiene al hilo siempre tenso. El hilo se apoya sobre una pequeña polea de radio despreciable situada en el extremo <math>B</math> de la barra, de forma que el tramo <math>\overline{BP}</math> permanece siempre paralelo al eje <math>OY</math> (ver figura). Se pide:
| |
| - |
| |
| - | # Ecuaciones horarias del punto <math>P</math>, <math>\overrightarrow{OP} = \vec{r}(t) =x(t) \vec{\imath} + y(t) \vec{\jmath}</math>.
| |
| - | # Instante del tiempo <math>t_M</math> en que la partícula alcanza su altura máxima.
| |
| - | # Radio de curvatura de la trayectoria seguida por <math>P</math>, en el instante considerado en el apartado anterior.
| |
| - |
| |
| - | ==[[2.4. Ejemplo de movimiento rectilíneo|Ejemplo de movimiento rectilíneo]]==
| |
| - | Una partícula efectúa un movimiento rectilíneo tal que si <math>x(t)</math> es la posición a lo largo de la recta y <math>v(t)</math> la componente de la velocidad en dicha
| |
| - | dirección, se cumple en todo instante
| |
| - |
| |
| - | <center><math>v = \sqrt{k x}</math></center>
| |
| - |
| |
| - | # Determine la aceleración en cada punto. ¿Qué tipo de movimiento efectúa la partícula?
| |
| - | # Si en <math>t=0</math> la partícula se encuentra en <math>x= x_0</math>, ¿cuál es su posición en cualquier instante posterior?
| |
| - |
| |
| - | ==[[2.5. Rectilíneo con desaceleración creciente (Ex.Nov/11)|Rectilíneo con desaceleración creciente (Ex.Nov/11)]]==
| |
| - | Una partícula está recorriendo el eje OX en sentido positivo con una celeridad constante de 25 m/s. En un instante dado (t=0) se detecta un obstáculo en su trayectoria a 50 m por delante de ella. A partir de dicho instante se le aplica a la partícula una desaceleración creciente en el tiempo según la fórmula <math>\,\vec{a}(t)=-Kt\,\vec{\imath}\,\,</math>, donde <math>K\,</math> es una constante de valor igual a 8.00 m/s<math>^{3}</math>. ¿Cuánto tiempo tardará en detenerse la partícula? ¿A qué distancia del obstáculo se detendrá?
| |
| - |
| |
| - | ==[[2.6. Tiro parabólico|Tiro parabólico]]==
| |
| - |
| |
| - | [[Archivo:tiroparabolico00.gif|right]]
| |
| - |
| |
| - | Supóngase el movimiento de un proyectil que se caracteriza por poseer una aceleración constante
| |
| - |
| |
| - | <center><math>\vec{a}(t)=-g\vec{k}</math></center>
| |
| - |
| |
| - | una posición inicial nula (<math>\vec{r}_0=\vec{0}</math>) y una velocidad inicial que forma un ángulo <math>\alpha</math> con la horizontal y tiene rapidez inicial <math>v_0</math>.
| |
| - |
| |
| - | # Determine el vector de posición, la velocidad y la aceleración en cada instante.
| |
| - | # Calcule la celeridad y el vector tangente en el instante en el cual el proyectil se encuentra a máxima altura.
| |
| - | # Halle la aceleración tangencial y la aceleración normal, así como el vector unitario normal, en el mismo instante del apartado anterior.
| |
| - | # Calcule el radio de curvatura y el centro de curvatura en el punto más alto de la trayectoria.
| |
| - |
| |
| - | ==[[2.7. Movimiento circular en torno a un eje oblicuo|Movimiento circular en torno a un eje oblicuo]]==
| |
| - | Una partícula gira alrededor de un eje que pasa por el origen de coordenadas y está orientado según la dirección y el sentido del vector <math>\vec{c}=\vec{\imath}+2\vec{\jmath}+2\vec{k}</math>. La aceleración angular de este movimiento es constante y de módulo 1 rad/s². La velocidad angular inicial es nula. Si en <math>t = 2\,\mathrm{s}</math> la partícula se encuentra en <math>\vec{r}=(-\vec{\imath}+\vec{\jmath}+4\vec{k})\,\mathrm{m}</math> calcule, para este instante
| |
| - |
| |
| - | # La velocidad y la aceleración.
| |
| - | # Las componentes intrínsecas de la aceleración.
| |
| - |
| |
| - | ==[[2.8. Ejemplo de movimiento helicoidal|Ejemplo de movimiento helicoidal]]==
| |
| - | Una partícula se mueve a lo largo de la hélice descrita por la ecuación paramétrica
| |
| - |
| |
| - | <center><math>\vec{r}(\theta)=A\cos(\theta)\vec{\imath}+A\,\mathrm{sen}(\theta)\vec{\jmath}+\frac{b\theta}{2\pi}\vec{k}</math></center>
| |
| - |
| |
| - | donde <math>A</math> y <math>b</math> son constantes conocidas. El movimiento de la partícula sigue la ley horaria
| |
| - |
| |
| - | <center><math>\theta(t) = \Omega_0 t + \beta t^2\,</math></center>
| |
| - |
| |
| - | donde <math>\Omega_0</math> y <math>\beta</math> son constantes conocidas.
| |
| - |
| |
| - | # Determine el parámetro arco de la hélice descrita, como función del parámetro <math>\theta</math> y del tiempo.
| |
| - | # Halle la rapidez del movimiento.
| |
| - | # Calcule la componente tangencial de la aceleración de la partícula en todo instante.
| |
| - | # Para el instante <math>t=0</math> calcule la velocidad y la aceleración de la partícula.
| |
| - | # Para el mismo instante, halle los vectores del triedro de Frenet, así como el radio de curvatura de la partícula y su aceleración normal.
| |
| - |
| |
| - | ==[[2.9. Movimiento descrito en coordenadas polares|Movimiento descrito en coordenadas polares]]==
| |
| - | En un plano descrito mediante coordenadas polares, se mueve una partícula conforme a las ecuaciones horarias
| |
| - |
| |
| - | <center><math>\rho(t)=A\cos(\omega t)\,;\,\,\,\,\,\,\,\,\theta(t)=\omega t\,</math></center>
| |
| - |
| |
| - | donde <math>A</math> y <math>\omega</math> son constantes conocidas.
| |
| - |
| |
| - | # Calcule la rapidez del movimiento.
| |
| - | # Halle el vector aceleración y sus componentes intrínsecas.
| |
| - | # Determine los vectores tangente y normal a la trayectoria en cada instante.
| |
| - | # Calcule el radio de curvatura.
| |
| - |
| |
| - | ==[[2.10. Movimiento en espiral descrito en polares (Ex.Nov/11)|Movimiento en espiral descrito en polares (Ex.Nov/11)]]==
| |
| - | Una partícula recorre una espiral logarítmica, estando su posición en cada instante de tiempo descrita en coordenadas polares mediante las ecuaciones horarias:
| |
| - |
| |
| - | <center><math>\rho(t)=\rho_0e^{-\omega t}\,;\,\,\,\,\,\,\,\,
| |
| - | \theta(t)=\omega t\,</math></center>
| |
| - |
| |
| - | donde <math>\rho_0\,</math> y <math>\omega\,</math> son constantes conocidas.
| |
| - |
| |
| - | # Calcule el vector velocidad y la rapidez del movimiento.
| |
| - | # Halle el vector aceleración y sus componentes intrínsecas.
| |
| - | # Calcule el radio de curvatura.
| |
| - |
| |
| - | ==[[No Boletín - Aceleración a partir de ley horaria y radio de curvatura (Ex.Oct/14)]]==
| |
| - | Una partícula recorre cierta curva parametrizada naturalmente, conociéndose la ley horaria y el valor del radio de curvatura (que es constante):
| |
| - | <center><math>
| |
| - | s(t)=A\,\mathrm{ln}\left(\frac{t}{t_0}\right)\,;\,\,\,\,\,\,\,\,\,\,\,\,R_{\kappa}(t)=A
| |
| - | \,\,\,\,\,\,\,\,\,\,\,\,\,\,\mathrm{(}A\,\,\mathrm{y}\,\,t_0\,\,\,\mathrm{son}\,\,
| |
| - | \mathrm{constantes}\,\,\mathrm{positivas}\,\,\mathrm{dadas)}
| |
| - | </math></center>
| |
| - |
| |
| - | # ¿Cuánto vale el módulo de su aceleración?
| |
| - | # Los datos conocidos permiten saber con certeza que este movimiento es... ('''Nota''': Sólo una opción es correcta)
| |
| - | <center><math> \mathrm{(A)}\,\,\mathrm{...retardado.}\,\,\,\,\, \mathrm{(B)}\,\,\mathrm{...circular.}\,\,\,\,\, \mathrm{(C)}\,\,\mathrm{...uniforme.}\,\,\,\,\, \mathrm{(D)}\,\,\mathrm{...helicoidal.}</math></center>
| |
| - |
| |
| - | ==[[No Boletín - Adelantamiento entre vehículos (Ex.Nov/11)]]==
| |
| - | Dos vehículos (A y B) avanzan por una misma carretera con celeridades variables en el tiempo pero tales que en todo instante se cumple que <math>\,v_B(t)=2\,v_A(t)</math>. El vehículo lento (A) va inicialmente por delante porque partió de un punto más adelantado. En cierto instante, y justo en una curva, el vehículo rápido (B) da alcance al lento (A). ¿Cuáles son las relaciones entre las respectivas aceleraciones tangenciales y entre las respectivas aceleraciones normales de ambos vehículos en el preciso instante del adelantamiento? ¿Son dichas relaciones necesariamente ciertas también para todo instante anterior o posterior al adelantamiento?
| |
| - |
| |
| - | ==[[No Boletín - Anilla ensartada en dos varillas (Ex.Nov/10)]]==
| |
| - | Una pequeña anilla <math>P</math> se encuentra ensartada en la intersección de dos barras giratorias. Los extremos fijos de las barras distan una cantidad <math>L</math>
| |
| - | y giran en el mismo sentido con la misma velocidad angular de módulo constante <math>\Omega</math> de forma que describen los ángulos indicados en la figura:
| |
| - |
| |
| - | <center>[[Archivo:anilla-dos-varillas.png]]</center>
| |
| - |
| |
| - | # ¿Cuáles son las ecuaciones horarias de <math>P</math>?
| |
| - | # ¿Qué clase de trayectoria describe?
| |
| - | # ¿Qué tipo de movimiento realiza?
| |
| - |
| |
| - | ==[[No Boletín - Automóviles con m.r.u. y m.r.u.a. (Ex.Nov/12)]]==
| |
| - | Un automóvil A recorre el eje OX con una velocidad constante <math>\,\vec{v}_A=72\,\vec{\imath} \,</math> km/h, hallándose en el punto <math>\,x=0\,\,</math> en el instante <math>\,t=0\,</math>. En ese mismo instante un segundo automóvil B, que se encontraba en reposo en el punto <math>\,x=d>0\,</math>, comienza a moverse con una aceleración constante <math>\,\vec{a}_B=0.8\,\vec{\imath}\,</math> m/s<math>^2</math>.
| |
| - |
| |
| - | ¿Cuál era la distancia <math>\,d\,\,</math> que separaba a ambos automóviles en el instante inicial si observamos que A logra alcanzar a B por un momento pero no llega a adelantarlo?
| |
| - |
| |
| - | ==[[No Boletín - Bólido con m.c.u. (Ex.Nov/12)]]==
| |
| - | La gravedad media en la superficie terrestre (g = 9.80665 m/s<math>^2</math>) es utilizada a veces como unidad de aceleración. Sea un bólido que recorre con celeridad constante un circuito circular de diámetro igual a 1500 yardas (1 yd = 0.9144 m) y que tarda exactamente 1 minuto en completar cada vuelta. ¿Cuánto vale la aceleración (en módulo) de dicho bólido expresada en la unidad g?
| |
| - |
| |
| - | ==[[No Boletín - Celeridad media a partir de celeridad instantánea (Ex.Nov/12)]]==
| |
| - | Un punto material recorre cierta trayectoria con una celeridad que varía en el tiempo según la fórmula:
| |
| - | <center><math>
| |
| - | v(t)=\frac{K}{t^3}\;\;\;\;\; \mathrm{(para}\,\,t>0\mathrm{)}
| |
| - | </math></center>
| |
| - | siendo <math>K\,</math> una constante de valor igual a <math>1 \,\mathrm{m}\cdot\mathrm{s}^2\,</math>
| |
| - |
| |
| - | ¿Cuál es la celeridad media del punto material en el intervalo de tiempo transcurrido entre <math>t=1\,\mathrm{s}\,</math> y <math>t=3\,\mathrm{s}\,</math>?
| |
| - |
| |
| - | ==[[No Boletín - Celeridad media a partir de ley horaria (Ex.Oct/13)]]==
| |
| - | Un punto material recorre cierta trayectoria parametrizada naturalmente con la siguiente ley horaria:
| |
| - | <center><math>
| |
| - | s(t)=\frac{K}{3T-t}\;\;\;\;\;\;\;\;\;\; \mathrm{(para}\,\,0\leq t\leq
| |
| - | T\mathrm{)}
| |
| - | </math></center>
| |
| - | siendo <math>K\,</math> y <math>T\,</math> sendas constantes conocidas.
| |
| - |
| |
| - | ¿Cuál es la celeridad media del punto material en el intervalo de tiempo transcurrido entre <math>t=0\,\,\,</math> y <math>\,\,t=T\,</math>?
| |
| - |
| |
| - | ==[[No Boletín - Celeridad media a partir de ley horaria II (Ex.Oct/15)]]==
| |
| - | Una partícula realiza un movimiento armónico simple con la siguiente ecuación horaria:
| |
| - | <center><math>
| |
| - | x(t)=-A\,\mathrm{cos}(\omega t)
| |
| - | </math></center>
| |
| - | donde la amplitud <math>\,A\,</math> y la pulsación <math>\,\omega\,</math> son constantes conocidas.
| |
| - |
| |
| - | ¿Cuál es la celeridad media de la partícula en el intervalo de tiempo transcurrido entre <math>\,t=0\,</math> y <math>\, t=\pi/\omega\,\,</math>?
| |
| - |
| |
| - | ==[[No Boletín - Celeridad media de un vehículo (Ex.Ene/12)]]==
| |
| - | Un automóvil recorre cierto trayecto del siguiente modo: la mitad de su longitud con celeridad constante de 120 km/h, y la otra mitad con celeridad constante de 60 km/h. ¿Cuál ha sido su celeridad media en el recorrido total?
| |
| - |
| |
| - | ==[[No Boletín - Celeridad media en viaje mixto (Ex.Jun/13)]]==
| |
| - | Un automóvil realiza un viaje de 100 km que consta de una primera parte sobre una carretera asfaltada y una segunda parte sobre un carril de tierra. En la carretera asfaltada avanza con una celeridad constante de 120 km/h, mientras que en el carril de tierra lo hace con una celeridad constante de 30 km/h. Sabiendo que la celeridad media en el trayecto total es de 75 km/h, ¿cuál es la longitud recorrida sobre el carril de tierra?
| |
| - |
| |
| - | ==[[No Boletín - Celeridad, aceleración tangencial y radio de curvatura (Ex.Nov/12)]]==
| |
| - | En el plano OXY, una partícula <math>\,P\,</math> recorre la trayectoria:
| |
| - | <center><math>
| |
| - | \overrightarrow{OP}\equiv\vec{r}(\psi)=R\,[1+\mathrm{cos}(\psi)\,]\,\vec{\imath}\,+R\,[\psi+\mathrm{sen}(\psi)\,]\,\vec{\jmath}</math>{{qquad}}{{qquad}}
| |
| - | (<math>R\,</math> es una constante conocida)</center>
| |
| - | siguiendo la ley horaria:
| |
| - | <center><math>
| |
| - | \psi(t)=\omega_0 t\,</math>{{qquad}}{{qquad}}(<math>\omega_0\,</math> es otra constante conocida)</center>
| |
| - |
| |
| - | Las tres preguntas siguientes se refieren al instante en el que <math>\,\psi=(\pi/3)\,\mathrm{rad}</math>.
| |
| - |
| |
| - | # ¿Cuál es la celeridad de la partícula en dicho instante?
| |
| - | # ¿Cuánto vale la componente tangencial de la aceleración en dicho instante?
| |
| - | # ¿Cuál es el radio de curvatura de la trayectoria en dicho instante?
| |
| - |
| |
| - | ==[[No Boletín - Celeridad, aceleración tangencial y radio de curvatura II (Ex.Oct/14)]]==
| |
| - | En el plano OXY, una partícula <math>P\,</math> se mueve conforme a la ecuación horaria:
| |
| - | <center><math>
| |
| - | \overrightarrow{OP}\equiv\vec{r}(t)=A\,\mathrm{sen}(\Omega t)\,\vec{\imath}\,-\,\frac{A}{2}\,\mathrm{cos}(2\,\Omega t)\,\vec{\jmath}
| |
| - | \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,
| |
| - | \mathrm{(}A\,\mathrm{y}\,\Omega\,\,\mathrm{son}\,\,\mathrm{constantes}\,\,\mathrm{conocidas)}
| |
| - | </math></center>
| |
| - | Las tres preguntas siguientes se refieren al instante <math>t=\displaystyle\frac{\pi}{6\,\Omega}\,</math>.
| |
| - |
| |
| - | # ¿Cuál es la celeridad de la partícula en dicho instante?
| |
| - | # ¿Cuánto vale la componente tangencial de su aceleración en dicho instante?
| |
| - | # ¿Cuál es el radio de curvatura de su trayectoria en dicho instante?
| |
| - |
| |
| - | ==[[No Boletín - Centro de curvatura y período de un circular uniforme (Ex.Oct/15)]]==
| |
| - | Desde un triedro cartesiano <math>\,OXYZ\,</math>, se observa a una partícula que realiza un movimiento circular uniforme. Periódicamente, la partícula pasa por el punto <math>\,O\,</math> (origen de coordenadas) con los siguientes valores instantáneos de velocidad y
| |
| - | aceleración:
| |
| - | <center><math>
| |
| - | \vec{v}=(2\,\vec{\imath}+8\,\vec{\jmath}+16\,\vec{k}\,)\,\,\mathrm{m}/\mbox{s}\,\,\,;\,\,\,\,\,\,\,\,\,\,\,\,
| |
| - | \vec{a}=(4\,\vec{\imath}+7\,\vec{\jmath}-4\,\vec{k}\,)\,\,\mathrm{m}/\mbox{s}^2
| |
| - | </math></center>
| |
| - |
| |
| - | # ¿Cuáles son las coordenadas del centro de curvatura de la trayectoria?
| |
| - | # ¿Cuál es el período del movimiento?
| |
| - |
| |
| - | ==[[No Boletín - Componentes intrínsecas en un movimiento circular (Ex.Jun/13)]]==
| |
| - | El ángulo <math>\psi\,</math> que forman entre sí los vectores velocidad y aceleración de una partícula puede determinarse a partir del cociente entre las componentes intrínsecas de su aceleración:
| |
| - |
| |
| - | <center><math>\mathrm{tg}(\psi)=\frac{a_n}{a_t}</math></center>
| |
| - |
| |
| - | Sea una partícula <math>P\,</math> que recorre la circunferencia de radio <math>R\,</math>:
| |
| - |
| |
| - | <center><math>\overrightarrow{OP}\equiv\vec{r}(\theta)=R\,\mathrm{cos}(\theta)\,\vec{\imath}+R\,\mathrm{sen}(\theta)\,\vec{\jmath}
| |
| - | </math></center>
| |
| - |
| |
| - | ¿Para cuál de las siguientes leyes horarias se mantiene constante a lo largo del tiempo el ángulo <math>\psi\,</math> formado por la velocidad y la aceleración de la partícula? (Nota: <math>\omega_0\,</math>, <math>\alpha_0\,</math> y <math>t_0\,</math> son constantes positivas conocidas.)
| |
| - |
| |
| - | 1) <math>\theta(t)=\mathrm{sen}(\omega_0 t)\,</math>
| |
| - |
| |
| - | 2) <math>\theta(t)=e^{(t/t_0)}</math>
| |
| - |
| |
| - | 3) <math>\theta(t)=\mathrm{ln}\left(\displaystyle\frac{t}{t_0}\right)</math>
| |
| - |
| |
| - | 4) <math>\theta(t)=\displaystyle\frac{1}{2}\alpha_0 t^{2}</math>
| |
| - |
| |
| - | ==[[No Boletín - Cuestión sobre movimiento de aceleración constante (Ex.Oct/14)]]==
| |
| - | Si una partícula se mueve de tal modo que su aceleración es un vector constante en el tiempo, ¿cuál de las siguientes afirmaciones es necesariamente cierta? ('''NOTA''': sólo una de las cuatro opciones es correcta).
| |
| - |
| |
| - | 1) La celeridad de la partícula varía linealmente con el tiempo.
| |
| - |
| |
| - | 2) La partícula realiza un movimiento rectilíneo uniformemente acelerado.
| |
| - |
| |
| - | 3) Es imposible que la partícula alcance un reposo instantáneo.
| |
| - |
| |
| - | 4) La trayectoria de la partícula es plana, aunque puede no ser recta.
| |
| - |
| |
| - | ==[[No Boletín - Cuestión sobre radio de curvatura (Ex.Oct/15)]]==
| |
| - | Una partícula, que se hallaba en reposo en el instante inicial (<math>t=0\,</math>), se mueve de tal modo que su aceleración tangencial y su aceleración normal son ambas constantes no nulas:
| |
| - | <center><math>
| |
| - | a_t(t)=C_1\neq 0\,;\,\,\,\,\,\,\,\,a_n(t)=C_2\neq 0
| |
| - | </math></center>
| |
| - |
| |
| - | ¿Cómo evoluciona el radio de curvatura de la trayectoria de esta partícula? ('''NOTA''': sólo una de las cuatro opciones es correcta).
| |
| - |
| |
| - | :(a) Es constante.
| |
| - | :(b) Aumenta linealmente con el tiempo.
| |
| - | :(c) Aumenta cuadráticamente con el tiempo.
| |
| - | :(d) Aumenta cúbicamente con el tiempo.
| |
| - |
| |
| - | ==[[No Boletín - Cuestión sobre velocidad y aceleración en el triedro de Frenet (Ex.Oct/13)]]==
| |
| - | Para un instante dado, se representan la velocidad <math>\vec{v}\,</math> y la aceleración <math>\vec{a}\,</math> de una partícula en sus orientaciones relativas a algún plano del triedro de Frenet <math>\{\vec{T},\vec{N},\vec{B}\}\,</math>. (Nota: se utiliza <math>\bigodot\,</math> para vectores perpendiculares al plano del papel y de sentido saliente, y <math>\bigotimes\,</math> para vectores perpendiculares al plano del papel y de sentido entrante).
| |
| - |
| |
| - | ¿Cuál es el diagrama correcto si se sabe que el movimiento es uniforme no rectilíneo?
| |
| - |
| |
| - | <center>[[Archivo:frenet-sol.png]]</center>
| |
| - |
| |
| - | ==[[No Boletín - Dos móviles sobre el eje OX acercándose (Ex.Oct/14)]]==
| |
| - | Un móvil A recorre el eje OX con una velocidad constante <math>\vec{v}_{A}=-\,25\,\vec{\imath}\,\,\,\mathrm{m}/\mathrm{s}\,</math>, hallándose en el punto <math>x=2\,\mathrm{km}\,</math> en el instante inicial <math>t=0\,</math>. En ese mismo instante un segundo móvil B, que se encuentra en reposo en el punto <math>x=0\,</math>, comienza a moverse con una aceleración creciente en el tiempo según la fórmula:
| |
| - | <center><math>
| |
| - | \vec{a}_B(t)=C\, t\,\vec{\imath}
| |
| - | </math></center>
| |
| - | donde <math>C\,</math> es una constante de valor igual a <math>2\,\mathrm{x}10^{-2}\,\mathrm{m}/\mathrm{s}^{3}\,</math>.
| |
| - |
| |
| - | # ¿Cuánto tiempo transcurre hasta el instante en el que la celeridad de B alcanza el mismo valor que la celeridad de A?
| |
| - | # ¿Qué distancia hay entre los móviles A y B en el instante al que se refiere la pregunta anterior?
| |
| - |
| |
| - | ==[[No Boletín - Ejemplo de movimiento circular no uniforme (Ex.Sep/11)]]==
| |
| - | Una partícula de masa <math>m</math> describe un movimiento circular de radio <math>R</math>, tal que su velocidad angular instantánea cumple
| |
| - |
| |
| - | <center><math>\omega = k\theta\,</math></center>
| |
| - |
| |
| - | con <math>k</math> una constante y <math>\theta</math> el ángulo que el vector de posición instantánea forma con el eje OX.
| |
| - |
| |
| - | # Determine la aceleración angular de la partícula como función del ángulo <math>\theta</math>.
| |
| - | # Halle las componentes intrínsecas de la aceleración lineal.
| |
| - | <!--
| |
| - | en <math>\theta = \pi/2</math> y <math>\theta = \pi</math>.
| |
| - |
| |
| - | # Calcule la fuerza neta que se ejerce sobre esta partícula para estos dos puntos; exprésela en la base cartesiana asociada al sistema de ejes OXY.
| |
| - | # Halle el trabajo que se realiza sobre la partícula entre esos dos puntos.
| |
| - | -->
| |
| - | <center>[[Archivo:particula-circunferencia.png|200px]]</center>
| |
| - |
| |
| - | ==[[No Boletín - Identificación de movimiento (Ex.Nov/10)]]==
| |
| - | Una partícula se mueve según las ecuaciones horarias
| |
| - |
| |
| - | <center><math>\vec{r}(t)=A\cos^2(\omega t)\vec{\imath}+2A\,\mathrm{sen}^2(\omega t)\vec{\jmath}+2A\cos^2(\omega t)\vec{k}</math></center>
| |
| - |
| |
| - | # ¿Qué trayectoria sigue la partícula?
| |
| - | # Determine la ley horaria <math>s(t)</math>. Suponga que <math>s(0)=0</math>.
| |
| - | # ¿Qué tipo de movimiento describe la partícula?
| |
| - |
| |
| - | ==[[No Boletín - Identificación de movimiento II (Ex.Nov/11)]]==
| |
| - | Un punto material se mueve con ecuación horaria:
| |
| - |
| |
| - | <center><math>\vec{r}(t)=12A\,\mbox{sen}(\omega t)\,\vec{\imath}+5A\,\mbox{sen}(\omega t)\,\vec{\jmath}+13A\,\mbox{cos}(\omega t)\,\vec{k}</math></center>
| |
| - |
| |
| - | donde <math>A\,</math> y <math>\omega\,</math> son constantes conocidas.
| |
| - |
| |
| - | # Determine la ley horaria <math>s(t)</math> suponiendo que <math>s(0)=0</math>.
| |
| - | # Determine el triedro de Frenet y el radio de curvatura en cada instante.
| |
| - | # Identifique el tipo de movimiento.
| |
| - |
| |
| - | ==[[No Boletín - Identificación de movimiento III (Ex.Oct/13)]]==
| |
| - | En el triedro cartesiano <math>OXYZ\,</math>, una partícula <math>P\,</math> se mueve conforme a la ecuación horaria:
| |
| - | <center><math>
| |
| - | \overrightarrow{OP}\equiv\vec{r}(t)=A\,\mathrm{sen}(\omega t)\,\mathrm{cos}(\omega t)
| |
| - | \,\vec{\jmath}+A\,\mathrm{cos}^2(\omega t)\,\vec{k}
| |
| - | </math></center>
| |
| - | donde <math>A\,</math> y <math>\omega\,</math> son constantes conocidas.
| |
| - |
| |
| - | # ¿Qué trayectoria sigue la partícula?
| |
| - | # ¿Con qué tipo de movimiento es recorrida dicha trayectoria?
| |
| - |
| |
| - | ==[[No Boletín - Movimiento circular con celeridad variable en el tiempo (Ex.Dic/12)]]==
| |
| - | Una partícula realiza un movimiento circular con celeridad variable en el tiempo conforme a la ley:
| |
| - | <center><math>
| |
| - | v=C\,t^{n}
| |
| - | </math></center>
| |
| - | donde <math>C\,</math> es una constante de valor igual a <math>0,5\,\mathrm{m/s}^{3}\,</math>.
| |
| - |
| |
| - | # ¿Cuál es el valor del exponente <math>n\,</math>?
| |
| - | # ¿Cómo varía durante este movimiento el cociente entre la aceleración normal y la aceleración tangencial de la partícula?
| |
| - |
| |
| - | ==[[No Boletín - Movimiento en espiral descrito en polares II (Ex.Oct/15)]]==
| |
| - | Una partícula recorre una espiral de Arquímedes, estando su posición en cada instante de tiempo descrita en coordenadas polares mediante las ecuaciones horarias:
| |
| - | <center><math>
| |
| - | \rho(t)=\rho_0+v_0\,t\,;\,\,\,\,\,\,\,\,
| |
| - | \theta(t)=\omega_0\, t
| |
| - | </math></center>
| |
| - | donde <math>\,\rho_0\,</math>, <math>\,v_0\,</math> y <math>\,\omega_0\,</math> son constantes positivas conocidas.
| |
| - |
| |
| - | # Determine la aceleración de la partícula expresada en la base polar.
| |
| - | # Calcule la aceleración tangencial de la partícula.
| |
| - |
| |
| - | ==[[No Boletín - Otro movimiento de partícula sujeta de un hilo (Ex.Sep/12)]]==
| |
| - |
| |
| - | [[Archivo:hilo-tenso.png|right]]
| |
| - |
| |
| - | La barra rígida <math>AB\,</math>, de longitud <math>L\,</math>, se halla contenida en el plano vertical <math>OXY\,</math> y rota alrededor de su extremo fijo <math>A\,</math>, cuya posición viene dada por <math>\,\overrightarrow{OA}=L\,\vec{\imath}</math>. Un hilo inextensible, de longitud <math>2L\,</math>, tiene uno de sus extremos conectado a un deslizador puntual <math>Q\,</math> que puede desplazarse sobre el eje vertical <math>OY\,</math>, mientras que del otro extremo cuelga una partícula <math>P</math> que mantiene al hilo tenso.
| |
| - |
| |
| - | El hilo se apoya sobre una pequeña polea de radio despreciable situada en el extremo <math>B</math> de la barra, y el movimiento del mecanismo es tal que el tramo <math>QB\,</math> permanece siempre paralelo al eje <math>OX\,</math>, y el tramo <math>BP\,</math> permanece siempre paralelo al eje <math>OY\,</math> (ver figura).
| |
| - |
| |
| - | # Determine el vector de posición de la partícula en función del ángulo que forma la barra <math>AB\,</math> con el eje <math>OX\,</math>, es decir, <math>\overrightarrow{OP}\equiv\vec{r}(\theta)</math>.
| |
| - | # Para la ley horaria <math>\theta(t)=\Omega\, t</math> (donde <math>\,\Omega\,</math> es una constante positiva conocida, y <math>\,0\leq\theta(t)\leq\pi/2</math>), halle los vectores velocidad y aceleración de la partícula <math>P</math> en función del tiempo.
| |
| - | # Sólo para el instante en que <math>\,\theta=\pi/4\,</math>, determine las componentes intrínsecas de la aceleración y el radio de curvatura de la partícula <math>P</math>.
| |
| - |
| |
| - | ==[[No Boletín - Otro tiro parabólico (Ex.Sep/15)]]==
| |
| - | Un proyectil se mueve en el plano vertical <math>OXZ\,</math>. Se conoce su aceleración constante (debida a su propio peso), y también su posición y su velocidad en el instante inicial (<math>t=0\,</math>):
| |
| - | <center><math>
| |
| - | \vec{a}(t)=-g\,\vec{k}\,\,\,;\,\,\,\,\,\,\,\,\,\,\,\,\vec{r}(0)=h\,\vec{k}\,\,\,;
| |
| - | \,\,\,\,\,\,\,\,\,\,\,\,\vec{v}(0)=v_0\,[\,\mathrm{cos}(\theta)\,\vec{\imath}+
| |
| - | \mathrm{sen}(\theta)\,\vec{k}\,]
| |
| - | </math></center>
| |
| - | donde <math>g\,</math>, <math>h\,</math> y <math>v_0\,</math> tienen valores positivos, y <math>\theta\,</math> está comprendido en el intervalo <math>0<\theta<\pi/2.\,</math>
| |
| - |
| |
| - | # Determine el radio de curvatura de la trayectoria del proyectil en el instante inicial.
| |
| - | # Determine la celeridad del proyectil en el instante en el que su trayectoria corta al eje <math>OX.\,</math>
| |
| - |
| |
| - | ==[[No Boletín - Rectilíneo con aceleración creciente (Ex.Oct/13)]]==
| |
| - | Una partícula, inicialmente en reposo en el origen de coordenadas, se mueve con una aceleración creciente en el tiempo según la fórmula:
| |
| - | <center><math>
| |
| - | \vec{a}(t)=3C t^2\,\vec{\jmath}
| |
| - | </math></center>
| |
| - | siendo <math>C\,</math> una constante de valor igual a <math>1\,\mathrm{m/s}^4\,</math>.
| |
| - | ¿A qué distancia del origen de coordenadas se hallará la partícula en el instante <math>t=2\,\mathrm{s}\,</math>?
| |
| - |
| |
| - | ==[[No Boletín - Rectilíneo con aceleración exponencialmente decreciente (Ex.Oct/15)]]==
| |
| - | Una partícula, que se hallaba en reposo en el instante inicial (<math>t=0\,</math>), se mueve con una aceleración exponencialmente
| |
| - | decreciente en el tiempo según la fórmula:
| |
| - | <center><math>
| |
| - | \vec{a}(t)=g\, e^{\displaystyle -\lambda\, t}\,\,\vec{\imath}
| |
| - | </math></center>
| |
| - | donde <math>\,g\,</math> y <math>\,\lambda\,</math> son constantes positivas conocidas.
| |
| - |
| |
| - | ¿Hacia qué valor límite tiende la velocidad de dicha partícula cuando se deja pasar mucho tiempo (<math>t\rightarrow\infty\!\,</math>) ?
| |
| - |
| |
| - | ==[[No Boletín - Rotación y traslación terrestres]]==
| |
| - | La Tierra rota uniformemente con respecto a su eje con velocidad angular <math>\omega</math> constante. Encuentre en función de la latitud <math>\lambda</math>, la velocidad y la aceleración de un punto sobre la superficie terrestre, debidas a dicha rotación (radio de la Tierra: <math>R = 6370\,\mathrm{km}</math>)
| |
| - |
| |
| - | Compare los módulos de los valores anteriores para el caso de un punto en el Ecuador, con los correspondientes al movimiento de traslación alrededor del Sol (distancia Tierra-Sol aproximadamente constante e igual a <math>d=0.15\,\mathrm{Tm}</math>).
| |
| - |
| |
| - | ==[[No Boletín - Valores instantáneos de velocidad y aceleración (Ex.Oct/13)]]==
| |
| - | En un instante dado, la velocidad y la aceleración de una partícula son las siguientes:
| |
| - | <center><math>
| |
| - | \vec{v}=(-2\,\vec{\imath}-2\,\vec{\jmath}+\vec{k}\,) \,\,\mathrm{m/s}\,\,;\,\,\,\,\,\,\,\,\,\,\,\, \vec{a}=-3\,\vec{k}
| |
| - | \,\,\mathrm{m/s}^2
| |
| - | </math></center>
| |
| - |
| |
| - | # ¿Cuánto vale en ese instante su aceleración tangencial?
| |
| - | # ¿Cuál es el radio de curvatura de la trayectoria en ese instante?
| |
| - |
| |
| - | <!--
| |
| - | ==[[Partícula oscilando en parábola]]==
| |
| - |
| |
| - | [[Archivo:particula-parabola.png|right]]
| |
| - |
| |
| - | Un punto material <math>P</math> se mueve en el plano <math>OXY</math> describiendo una trayectoria parabólica de ecuación <math>y^2 = (b^2/a) x</math>. Se sabe que la partícula se halla inicialmente en reposo en la posición <math>x=a</math>, <math>y=b</math>; y que la componente <math>y</math> de su aceleración verifica en todo instante la expresión: <math>a_y =-k^2 y</math> (con ''k'' = cte). Determine en función del tiempo la posición, velocidad y aceleración. ¿Cuál es la siguiente posición de reposo, y cuánto tiempo tarda en alcanzarla?
| |
| - |
| |
| | ==[[Cinemática del tiro parabólico]]== | | ==[[Cinemática del tiro parabólico]]== |
| | | | |
| | [[Archivo:tiroparabolico00.gif|right]] | | [[Archivo:tiroparabolico00.gif|right]] |
| | | | |
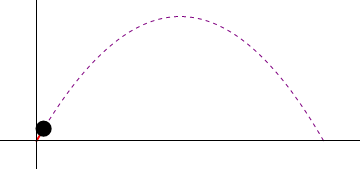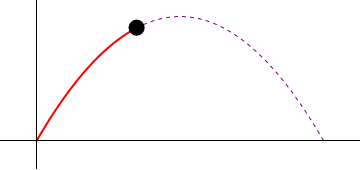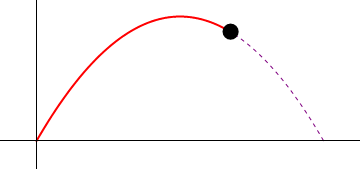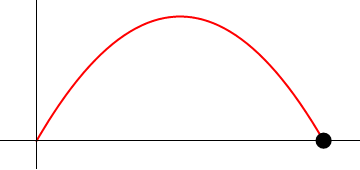
| - | Supóngase el movimiento de un proyectil que se caracteriza por poseer una aceleración constante | + | Supóngase el movimiento de un proyectil, dado en coordenadas cartesianas por |
| | | | |
| - | <center><math>\vec{a}(t)=-g\vec{k}</math></center> | + | <center><math>x=(v_0\cos\alpha)t\,</math>{{qquad}}{{qquad}}<math>y=0\,</math>{{qquad}}{{qquad}}<math>z=(v_0\,\mathrm{sen}\,\alpha)t-\frac{1}{2}gt^2</math></center> |
| - | | + | |
| - | una posición inicial nula (<math>\vec{r}_0=\vec{0}</math>) y una velocidad inicial que forma un ángulo <math>\alpha</math> con la horizontal y tiene rapidez inicial <math>v_0</math>.
| + | |
| | | | |
| | # Determine el vector de posición, la velocidad y la aceleración en cada instante. | | # Determine el vector de posición, la velocidad y la aceleración en cada instante. |
| | # Calcule la celeridad y el vector tangente en el instante inicial, en el instante en que se encuentra a mayor altura y en el momento en que vuelve a impactar con el suelo. | | # Calcule la celeridad y el vector tangente en el instante inicial, en el instante en que se encuentra a mayor altura y en el momento en que vuelve a impactar con el suelo. |
| | # Halle la aceleración tangencial y la aceleración normal, así como el vector unitario normal en los tres instantes anteriores. | | # Halle la aceleración tangencial y la aceleración normal, así como el vector unitario normal en los tres instantes anteriores. |
| - | # Calcule el radio de curvatura y el centro de curvatura en el punto más alto de la trayectoria. | + | # Calcule el radio de curvatura y el centro de curvatura en los mismos tres instantes. |
| - | # Para este mismo punto, halle las componentes intrínsecas de la velocidad y la aceleración, así como el radio de curvatura, si <math>\alpha = 45^\circ</math>, <math>v_0=25.0\,\mathrm{m}/\mathrm{s}</math> y <math>g=9.81\,\mathrm{m}/\mathrm{s}^2</math>.
| + | |
| - | | + | |
| - | ==Más problemas==
| + | |
| - | ===[[Movimiento cicloidal]]===
| + | |
| - | Una ''cicloide'' es la curva que describe un punto del borde de un disco que rueda sobre una superficie plana.
| + | |
| - | | + | |
| - | Suponga que tenemos un disco de radio <math>R</math> que rueda uniformemente sobre una línea horizontal. Deseamos analizar la trayectoria del punto del borde que toca la superficie en la posición inicial.
| + | |
| - | | + | |
| - | Si la velocidad del centro del disco es <math>\vec{v}_C=v_0\vec{\imath}</math>,
| + | |
| - | | + | |
| - | # ¿Cuanto ha avanzado el disco entre <math>t=0</math> y un instante <math>t</math>? ¿Cuánto ha girado? ¿Cuál es la posición <math>\vec{r}(t)</math> del punto P del disco que se encontraba en contacto con el suelo en <math>t=0</math>?
| + | |
| - | # Para este mismo punto P determine su velocidad y aceleración en cada instante.
| + | |
| - | # Halle la ley horaria que sigue el punto P. ¿Cuál es la distancia total recorrida por este punto cuando el disco completa una vuelta?
| + | |
| - | # Determine las componentes intrínsecas de la aceleración, el radio de curvatura y la posición del centro de curvatura para el mismo periodo anterior.
| + | |
| - | | + | |
| - | ===[[Espiral logarítmica]]===
| + | |
| - | Una partícula recorre la espiral logarítmica de ecuación
| + | |
| - | | + | |
| - | <center><math>\vec{r} = b (\cos(\theta)\vec{\imath}+\,\mathrm{sen}\,(\theta)\vec{\jmath})\mathrm{e}^{-k\,\theta}</math></center>
| + | |
| - | | + | |
| - | donde <math>b</math> y <math>k</math> son constantes. El movimiento es uniforme a lo largo de la curva, con celeridad constante <math>v_0\,</math>. En el instante inicial la partícula se encuentra en <math>\theta=0</math>
| + | |
| | | | |
| - | # Determine la ley horaria <math>\theta = \theta(t)</math>.
| + | [[Categoría:Problemas de cinemática de la partícula|0]] |
| - | # Calcule el tiempo que tarda en llegar a <math>\vec{r}=\vec{0}</math>. ¿Cuántas vueltas da para ello?
| + | [[Categoría:Cinemática de la partícula]] |
| - | # Halle el vector aceleración y sus componentes intrínsecas en cada punto de la trayectoria.
| + | |
| - | # Determine la posición de los centros de curvatura de este movimiento.
| + | |
| - | -->
| + | |
| - | [[Categoría:Problemas de cinemática del punto material (G.I.T.I.)|0]] | + | |
| - | [[Categoría:Cinemática del punto material (G.I.T.I.)]] | + | |
| - | [[Categoría:Problemas de Física I (G.I.T.I.)|3]]
| + | |