Esfera conductora sumergida en dieléctrico

De Laplace

(Diferencias entre revisiones)

Revisión de 23:40 19 jun 2010

Contenido

1 Enunciado
2 Potencial y campo eléctrico
3 Vector desplazamiento y carga libre
4 Distribuciones de carga
5 Energía almacenada
6 Variación de energía y trabajo del generador
7 Anexo: discusión sobre la simetría de la solución

1 Enunciado

Una esfera conductora de radio $a$ se encuentra conectada a una fuente de tensión de valor $V 0$ . La esfera se encuentra semisumergida en un líquido dieléctrico ideal de permitividad $\varepsilon$ .

Obtenga la expresión del potencial electrostático y del campo eléctrico en todo el espacio. Suponga que el potencial sólo depende de la distancia al centro de la esfera.
Obtenga la expresión del vector desplazamiento en todo el espacio. Calcule la cantidad de carga libre en la esfera conductora.
Determine las distribuciones de carga libre y de polarización que hay en el sistema descrito.
Calcule la energía electrostática almacenada en el sistema.
Si, sin desconectar la fuente, se retira el líquido dieléctrico, ¿cuánto cambia la energía almacenada? ¿Cuánto trabajo realiza el generador?

2 Potencial y campo eléctrico

2.1 Planteamiento general

Con el fin de facilitar la descripción del sistema bajo estudio, adoptaremos un sistema de referencia cuyo origen O coincida con el centro de la esfera condutora de radio a, y cuyo OZ sea perpendicular a la superficie plana definida por la interfaz entre el vacío y el líquido dieléctrico lineal de permitividad dieléctrica $\displaystyle \varepsilon$ . De esta forma, la superficie $\partial\mathrm{C}$ de la esfera conductora y la interfaz

Σ

entre los dieléctricos estarán descritas en coordenadas esféricas por las expresiones $\partial \mathrm{C}:\ r=a$ ; $\Sigma: \theta=\frac{\pi}{2}\;\; (r>a)$

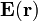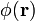Asumiendo que el sistema se halla en equilibrio electrostático cuando la esfera conductora está conectada a la fuente de tensión constante, se tendrá que el campo eléctrico $\mathbf{E}(\mathbf{r})$ es irrotacional y deriva, por tanto de un potencial electrostático $\phi(\mathbf{r})$ ,

$\nabla\times\mathbf{E}=\mathbf{0}\quad\Longleftrightarrow\quad\mathbf{E}=-\nabla\phi$

Además, tanto si el conductor consiste en una esfera conductora maciza, o bien presenta huecos (pero sin carga eléctrica en su interior), el campo eléctrico en toda la región $r < a$ debe ser nulo. En consecuencia, el potencial va a ser constante, y como este campo escalar debe ser continuo, el valor del potencial en el interior de la esfera conductora va a ser igual al que tiene en $\partial\mathrm{C}$ , que es superficie equipotencial de valor $V 0$ , fijado por la fuente. Por otra parte, considerando que el interior de la esfera (maciza o hueca) es un medio lineal que se comporta como un conductor ideal, se tendrá que el vector desplazamiento es también nulo en dicha región:

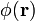$\mathbf{E}(|\mathbf{r}|<a)=\mathbf{0}\mathrm{;}\qquad\phi(|\mathbf{r}|<a)=\phi(|\mathbf{r}|=a^+)=V_0\mathrm{;}\qquad\mathbf{D}(|\mathbf{r}|<a)=\mathbf{0}$

Este resultado está directamente relacionado con la ausencia de carga eléctrica neta (libre o de polarización) en los puntos del interior de la esfera; sin embargo, en la superficie conductora $\partial\mathrm{C}$ , sí van a existir distribuciones de carga eléctrica, vinculadas a la discontinuidad de la componente normal del campo eléctrico sobre dicha superficie. Y es que entre la superficie de la esfera (a potencial $V 0$ ) y el infinito (donde $\phi(\mathbf{r})$ se anula), existe un gradiente de potencial y, en consecuencia, un campo eléctrico 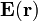$\mathbf{E}(\mathbf{r})$ . Las fuentes escalares de este campo serán las distribuciones de carga eléctrica (libres y de polarización) existentes en la superficie de la esfera conductora, así como las cargas de polarización que pudiese haber en la región ocupada por el líquido dieléctrico. Obsérvese que si éste es un dieléctrico ideal, no puede contener cargas libres; por otra parte, en el semiespacio vacío no va a existir ningún tipo de carga eléctrica.

2.2 Ecuación para el potencial

En el espacio exterior a la esfera conductora , ocupado por sendos medios que presentan comportamiento dieléctrico lineal, las ecuaciones que determinan los campos electrostáticos y la relación constitutiva que los relaciona son

$\nabla\cdot\mathbf{D}=\rho_l(\mathbf{r})\ \mathrm{;}$ $\nabla\times\mathbf{E}=\mathbf{0}\ \mathrm{;}$ $\mathbf{D}(\mathbf{r})=\varepsilon(\mathbf{r}) \mathbf{E}(\mathbf{r})$

donde $ρ l$ es la densidad volumétrica de carga eléctrica libre y $\varepsilon(\mathbf{r})$ es la permitividad dieléctrica del medio. Según se discutió en el apartado anterior, no puede haber carga eléctrica libre en la región exterior a la esfera conductora( $r > a$ ); además, dicha región puede considerarse como un medio inhomogéneo formado por el semiespacio vacío y el ocupado por el líquido dieléctrico. Por tanto, se tendrá que

$\displaystyle\rho_l(r>a)=0\ \mathrm{;}$ $\varepsilon(\mathbf{r})=\left\{\begin{array}{l}\varepsilon_0\mathrm{;}\;\;\;\mathrm{si}\;\; r>a\;\;\mathrm{y}\;\; 0\le\theta<\pi/2\\ \\ \varepsilon\mathrm{;}\;\;\;\mathrm{si}\;\; r>a\;\;\mathrm{y}\;\; \pi/2<\theta\le\pi\end{array}\right.$

Teniendo en cuenta ahora que el campo eléctrico es irrotacional y, por tanto, deriva de un potencial electrostático, la ecuación de la divergencia del vector desplazamiento lleva al siguiente resultado:

$\nabla\cdot\mathbf{D}=0\quad\Longrightarrow\quad$ $\nabla\cdot\left[\varepsilon(\mathbf{r})\nabla\phi\right]=0\quad\Longrightarrow\quad\left\{\begin{array}{l}\nabla\cdot(\varepsilon_0\nabla\phi)=0\mathrm{;}\;\;\;\mathrm{en}\;\; r>a\;\;\mathrm{y}\;\; 0\le\theta<\pi/2\\ \\ \nabla\cdot(\varepsilon\nabla\phi)=0\mathrm{;}\;\;\;\mathrm{en}\;\; r>a\;\;\mathrm{y}\;\; \pi/2<\theta\le\pi\end{array}\right.$

Y como las permitividades $\varepsilon_0$ y $\varepsilon$ son constantes en su correspondiente semiespacio, ambas ecuaciones llevan a que el potencial electrostático verifica la ecuación de Laplace, tanto en el vacío como en el líquido dieléctrico.

$\nabla^2\phi(\mathbf{r})=0\ \mathrm{;}\;\;\; \forall\;\; |\mathbf{r}|>a$

En principio cabría pensar que la solución a esta ecuación podría ser una distinta en cada dieléctrico; sin embargo, en el enunciado se indica que el potencial es sólo función de la variable $r$ . Es decir, el valor del potencial en un punto sólo va a depender de la distancia $\ r$ a que se encuentre del centro de la esfera, independientemente del semiespacio en que se halle. Como se puede comprobar en el anexo final, ésta no va a ser una mera suposición que permite obtener un resultado analítico sencillo, más o menos aproximado a la solución exacta, sino que lleva a dicha solución exacta.

En definitiva, la solución al problema del potencial para $\ r>a$ es una función de la forma $\ \phi(r)$ , que verifica la ecuación de Laplace y las condiciones de contorno fijadas en sistema:

$\frac{1}{r^2}\frac{d}{dr}\left(r^2\frac{d\phi}{dr}\right)=0\mathbf{,}\;\;\;\mathrm{para}\;\;r>a\mathbf{;}\qquad\phi(r=a)=V_0\mathbf{;}\;\;\;\phi(r\rightarrow\infty)=0$

2.3 Potencial eléctrico

Puesto que el punto singular correspondiente al valor $\ r=0$ no pertenece al dominio donde se busca la solución de la anterior ecuación diferencial, la integral primera de ésta será

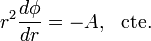
$r^2\frac{d\phi}{dr}=-A\mathrm{,}\;\;\; \mathrm{cte.}$

La función solución al problema del potencial en la región dieléctrica inhomogénea, exterior a la esfera conductora, será de la forma

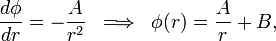
$\frac{d\phi}{dr}=-\frac{A}{r^2}\;\;\Longrightarrow\;\;\phi(r)=\frac{A}{r}+B\mathrm{,}$

donde las constantes $\ A$ y $\ B$ se determinan a partir de las condiciones de contorno:

$\left.\begin{array}{r}\displaystyle \phi(r=a)=\frac{A}{a}+B=V_0\\ \\ \phi(r\rightarrow\infty)=B=0\end{array}\right\}\, \Longrightarrow\;A=V_0 a \mathrm{;}\;\;\;B=0$

Este resultado, junto con el discutido en el apartado dedicado al planteamiento general del problema, nos lleva a formular la función de campo

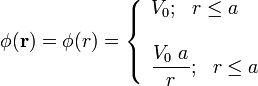
$\phi(\mathbf{r})=\phi(r)=\left\{\begin{array}{l}V_0\mathrm{;}\;\;\;r\le a\\ \\ \displaystyle\frac{V_0\ a}{r}\mathrm{;}\;\;\;r\le a\end{array}\right.$

que describe el potencial electrostático creado en todos los puntos del espacio por el sistema bajo estudio.

2.4 Campo eléctrico

Como ya se discutió en el planteamiento general del problema, el campo electrostático es, en cada punto el vector opuesto al gradiente del potencial; por tanto,

No se pudo entender (Falta el ejecutable de <strong>texvc</strong>. Por favor, lea <em>math/README</em> para configurarlo.): \mathbf{E}(\mathbf{r})=-\nabla\phi(\mathbf{r})=\left\{\begin{array}{l}\mathbf{0}\mathrm{;}\;\;\;r\le a\\ \\ \displaystyle\-frac{d\phi}{dr}=frac{V_0\ a}{r^2}\mathrm{;}\;\;\;r\le a\end{array}\right.

3 Vector desplazamiento y carga libre

4 Distribuciones de carga

5 Energía almacenada

6 Variación de energía y trabajo del generador

7 Anexo: discusión sobre la simetría de la solución

Obsérvese que el sistema bajo estudio no tiene simetría esférica, pues ésta es rota por la discontinuidad entre el vacío y el líquido dieléctrico, que se verfica en el plano $\ \theta=\pi/2$ (es decir, en $\ z=0$ ). No obstante, sí presenta simetría cilíndrica, pues las propiedades del sistema van a ser invariantes en la coordenada $\varphi$ . Por tanto, el potencial electrostático podrá ser, en principio, función de las coordenadas cilíndricas, $\ \phi(\rho,z)$ , o bien $\ \phi(r,\theta)$ si utilizamos las esféricas. Obsérvese que la existencia de soluciones distintas en cada medio,

$\phi(r,\theta)=\left\{\begin{array}{l}\phi_\mathrm{vac}(r)\mathrm{;}\;\;\;\mathrm{en}\;\; r\ge a\;\;\mathrm{y}\;\; 0\le\theta<\pi/2\\ \\ \phi_\mathrm{liq}(r)\mathrm{;}\;\;\;\mathrm{en}\;\; r\ge a\;\;\mathrm{y}\;\; \pi/2<\theta\le\pi\end{array}\right.$

está indicando una dependencia implícita de la solución con el parámetro $\ \theta$ .

Sin embargo, revisemos las condiciones de contorno que debe verificar el potencial. En la superficie esférica conductora debe valer $\ V_0$ , mientras que cuando $\ r\rightarrow \infty$ dicho campo escalar debe anularse, independientemente del valor de $\ \theta$ :

$\phi_\mathrm{vac}(r=a)=\phi_\mathrm{liq}(r=a)=V_0\mathrm{;}\qquad\phi_\mathrm{vac}(r\rightarrow\infty)=\phi_\mathrm{liq}(r\rightarrow\infty)=0$

Por otra parte, el potencial debe ser continuo en la interfaz $\ \Sigma$ que separa el vacío y el líquido dieléctrico, de manera que

$\phi_\mathrm{vac}(r)\big\rfloor_{\theta=\frac{\pi}{2}^-}=\phi_\mathrm{liq}(r)\big\rfloor_{\theta=\frac{\pi}{2}^+}\;\;\;\forall\;\; r>a$

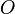Luego si las soluciones al potencial en el vacío y en el líquido verifican la misma ecuación (la ecuación de Laplace) y las mismas condiciones de contorno, sus expresiones deben ser idénticas. O lo que es lo mismo, podemos proponer una función $\ \phi(r)$ , que sólo depende de la distancia $\ r$ al punto $\ O$ , como solución al problema del potencial en el espacio exterior a la esfera conductora.

Comprobemos ahora que los campos vectoriales que se derivan de este potencial verifican correctamente las condiciones de continuidad y salto en la interfaz 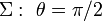$\ \Sigma:\ \theta=\pi/2$ :

$\mathbf{n}\times\left[\mathbf{E}\big\rfloor_{\theta=\frac{\pi}{2}^+}-\mathbf{E}\big\rfloor_{\theta=\frac{\pi}{2}^-}\right]_\Sigma=\mathbf{0}\ \mathrm{;}\qquad \mathbf{n}\cdot\left[\mathbf{D}\big\rfloor_{\theta=\frac{\pi}{2}^+}-\mathbf{D}\big\rfloor_{\theta=\frac{\pi}{2}^-}\right]_\Sigma=\sigma_l\big\rfloor_\Sigma$

donde $\ \mathbf{n}$ es el vector normal a dicha superficie, en el sentido creciente de la variable $\ \theta$ ; es decir,

$\mathbf{n}\big\rfloor_\Sigma=\mathbf{u}_\theta(\theta=\pi/2;\varphi)=-\mathbf{u}_z$

Por su parte, $\ \sigma_l\big\rfloor_\Sigma$ , es la densidad superficial de carga eléctrica libre en $\ \Sigma$ . Como se discutió en el primer apartado, esta densidad va a ser nula en todos los puntos por tratarse de una interfaz entre dos medios considerados como dieléctricos ideales.

El campo eléctrico que se deriva del potencial $\ \phi(r)$ va a ser radial y, por tanto, paralelo a la interfaz $\ \Sigma$ en todos sus puntos. Si el potencial es la misma función $\ \phi(r)$ para todo el espacio, la componente radial (la única), no es función de $\ \theta$ y se tendrá,

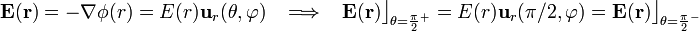
$\mathbf{E}(\mathbf{r})=-\nabla \phi (r)=E(r)\mathbf{u}_r(\theta,\varphi)\;\;\;\Longrightarrow\;\;\;\mathbf{E}(\mathbf{r})\big\rfloor_{\theta=\frac{\pi}{2}^+}=E(r)\mathbf{u}_r(\pi/2,\varphi)=\mathbf{E}(\mathbf{r})\big\rfloor_{\theta=\frac{\pi}{2}^-}$

verificándose, por tanto, la continuidad de la componente del campo eléctrico que es tangencial a la interfaz $\ \Sigma$ .

En cuanto al vector desplazamiento, también va tener la dirección radial en cada punto, sin embargo, su componente en dicha dirección va a depender del medio:

$\mathbf{D}(\mathbf{r})=\varepsilon(\mathbf{r})\mathbf{E}(\mathbf{r})=\left\{\begin{array}{l}\varepsilon_0E(r)\mathbf{u}_r(\theta,\varphi)\mathrm{;}\;\;\;\mathrm{en}\;\; r>a\;\;\mathrm{y}\;\; 0\le\theta<\pi/2\\ \\ \varepsilon E(r)\mathbf{u}_r(\theta,\varphi)\mathrm{;}\;\;\;\mathrm{en}\;\; r>a\;\;\mathrm{y}\;\; \pi/2<\theta\le\pi\end{array}\right.$

Por tanto, el vector desplazamiento es tangente al plano $\ \Sigma: \theta=\pi/2$ , aunque el módulo va a ser distinto a un lado y otro:

$\mathbf{D}(\mathbf{r})\big\rfloor_{\theta=\frac{\pi}{2}^+}=\varepsilon E(r)\mathbf{u}_r(\pi/2,\varphi)\neq\varepsilon_0 E(r)\mathbf{u}_r(\pi/2,\varphi)=\mathbf{D}(\mathbf{r})\big\rfloor_{\theta=\frac{\pi}{2}^-}$

Es decir, sufre una discontinuidad en dicha superficie. La ausencia de carga libre en la interfaz entre el vacío y el líquido dieléctrico tiene como consecuencia que las componentes normales del vector desplazmamiento deben ser continuas, lo cuál es compatible con el resultado anterior donde obtuvimos que dicho vector va a ser puramente tangencial, de manera que

$\mathbf{n}\big\rfloor_\Sigma\perp\mathbf{D}(\mathbf{r})\big\rfloor_{\theta=\frac{\pi}{2}^\pm}\;\;\;\Longrightarrow\;\;\; \mathbf{n}\cdot\left[\mathbf{D}\big\rfloor_{\theta=\frac{\pi}{2}^+}-\mathbf{D}\big\rfloor_{\theta=\frac{\pi}{2}^-}\right]_\Sigma=0$

@@ Línea 73: / Línea 73: @@
 Como ya se discutió en el planteamiento general del problema, el campo electrostático es, en cada punto el vector opuesto al gradiente del potencial; por tanto,
-<center><math>\mathbf{E}(\mathbf{r})=-\nabla\phi(\mathbf{r})=\left\{\begin{array}}l}\mathbf{0}\mathrm{;}\;\;\;r\le a\\ \\ \displaystyle\-frac{d\phi}{dr}=frac{V_0\ a}{r^2}\mathrm{;}\;\;\;r\le a\end{array}\right.</math></center>
+<center><math>\mathbf{E}(\mathbf{r})=-\nabla\phi(\mathbf{r})=\left\{\begin{array}{l}\mathbf{0}\mathrm{;}\;\;\;r\le a\\ \\ \displaystyle\-frac{d\phi}{dr}=frac{V_0\ a}{r^2}\mathrm{;}\;\;\;r\le a\end{array}\right.</math></center>
 ==Vector desplazamiento y carga libre==

Esfera conductora sumergida en dieléctrico

De Laplace

Revisión de 23:40 19 jun 2010

Contenido

1 Enunciado

2 Potencial y campo eléctrico

2.1 Planteamiento general

2.2 Ecuación para el potencial

2.3 Potencial eléctrico

2.4 Campo eléctrico

3 Vector desplazamiento y carga libre

4 Distribuciones de carga

5 Energía almacenada

6 Variación de energía y trabajo del generador

7 Anexo: discusión sobre la simetría de la solución

Herramientas:

Buscar

Vistas

Herramientas

Herramientas personales

Navegación

SEARCH

TOOLBOX

LANGUAGES