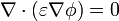Esfera conductora sumergida en dieléctrico
De Laplace
(Diferencias entre revisiones)
(→Planteamiento) |
(→Planteamiento) |
||
| Línea 13: | Línea 13: | ||
==Potencial y campo eléctrico== | ==Potencial y campo eléctrico== | ||
===Planteamiento=== | ===Planteamiento=== | ||
| - | [[Archivo:fi1_p1_2p_09_10.png|left]]Con el fin de facilitar la descripción del sistema bajo estudio, adoptaremos un sistema de referencia cuyo origen ''O'' coincida con el centro de la esfera condutora de radio ''a'', y cuyo ''OZ'' sea perpendicular a la superficie plana definida por la interfaz entre el vacío y el líquido dieléctrico lineal de permitividad dieléctrica <math>\displaystyle \varepsilon</math>. De esta forma la superficie <math> | + | [[Archivo:fi1_p1_2p_09_10.png|left]]Con el fin de facilitar la descripción del sistema bajo estudio, adoptaremos un sistema de referencia cuyo origen ''O'' coincida con el centro de la esfera condutora de radio ''a'', y cuyo ''OZ'' sea perpendicular a la superficie plana definida por la interfaz entre el vacío y el líquido dieléctrico lineal de permitividad dieléctrica <math>\displaystyle \varepsilon</math>. De esta forma, la superficie <math>\partial\mathrm{C}</math> de la esfera conductora y la interfaz <math>\Sigma</math> entre los dieléctricos estarán descritas en coordenadas esféricas por las expresiones |
| - | <center><math>\partial \mathrm{C}:\ r=a</math></center> | + | <center><math>\partial \mathrm{C}:\ r=a</math>; \qquad <math>\Sigma: \theta=\frac{\pi}{2}\,\mathrm{(}r>a\mathrm{)} </math></center> |
===Ecuación para el potencial=== | ===Ecuación para el potencial=== | ||
Revisión de 12:35 17 jun 2010
Contenido |
1 Enunciado
Una esfera conductora de radio a se encuentra conectada a una fuente de tensión de valor V0. La esfera se encuentra semisumergida en un líquido dieléctrico ideal de permitividad 
.
- Obtenga la expresión del potencial electrostático y del campo eléctrico en todo el espacio. Suponga que el potencial sólo depende de la distancia al centro de la esfera.
- Obtenga la expresión del vector desplazamiento en todo el espacio. Calcule la cantidad de carga libre en la esfera conductora.
- Determine las distribuciones de carga libre y de polarización que hay en el sistema descrito.
- Calcule la energía electrostática almacenada en el sistema.
- Si, sin desconectar la fuente, se retira el líquido dieléctrico, ¿cuánto cambia la energía almacenada? ¿Cuánto trabajo realiza el generador?
2 Potencial y campo eléctrico
2.1 Planteamiento
. De esta forma, la superficie 
de la esfera conductora y la interfaz Σ entre los dieléctricos estarán descritas en coordenadas esféricas por las expresiones
; \qquad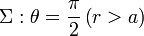 
2.2 Ecuación para el potencial
Las ecuaciones que determinan los campos en presencia de dieléctricos lineales son
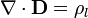
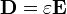
En este caso tenemos que las únicas cargas libres son las situadas sobre la esfera conductora, por lo que tanto en el vacío como en el líquido dieléctrico se cumple
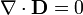
La condición de que el campo electrostático es irrotacional implica que deriva de un potencial
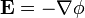
Sustituyendo esta relación y la ley constitutiva en la ley de Gauss para cada región queda
