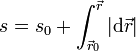Cinemática de la partícula (G.I.T.I.)

De Laplace

(Diferencias entre revisiones)

Revisión de 16:47 31 may 2010

1 Introducción

1.1 Cinemática

1.2 Partícula

1.3 Sistema de referencia

2 Trayectoria y ley horaria

2.1 Posición instantánea

Cuando una partícula se mueve por el espacio en cada instante ocupará una posición, que irá cambiando de forma continua con el tiempo (ya que la partícula no puede dematerializarse o teleportarse a otra posición).

En principio podemos etiquetar cada posición por una letra A, B, C,... Sin embargo, es más práctico identificar cada posición por su vector de posición cuyas componentes cartesianas son las distancias a los planos coordenados

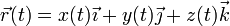
$\vec{r}(t) = x(t)\vec{\imath}+y(t)\vec{\jmath}+z(t)\vec{k}$

Aquí $x (t)$ , $y (t)$ y $z (t)$ son ciertas funciones continuas del tiempo.

Cuando se da la posición de la partícula como función del tiempo se dice que se conocen las ecuaciones horarias del movimiento.

2.2 Desplazamiento

El desplazamiento de una partícula en un intervalo $Δ t$ es la diferencia (vectorial) entre la posición al final del intervalo y la posición inicial

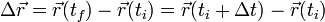
$\Delta \vec{r}= \vec{r}(t_f)-\vec{r}(t_i)=\vec{r}(t_i+\Delta t)-\vec{r}(t_i)$

Es importante hacer la distinción entre el desplazamiento y la distancia recorrida. Una partícula que recorra una curva cerrada tendrá un desplazamiento nulo, aunque la distancia recorrida no sea nula.

2.3 Desplazamiento diferencial=

Cuando tenemos un desplazamiento entre dos instantes muy próximos,separados un intervalo $d t$ , se dice que tenemos un desplazamiento diferencial

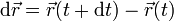
$\mathrm{d}\vec{r}=\vec{r}(t+\mathrm{d}t)-\vec{r}(t)$

Desde el punto de vista matemático, la palabra diferencial implica el proceso de tomar el límite 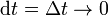$\mathrm{d}t = \Delta t\to 0$ , con lo que técnicamente un desplazamiento diferencial tiene longitud nula. Sin embargo, desde el punto de vista práctico, es más sencillo considerar un desplazamiento diferencial como de longitud muy pequeña comparada con las distancias típicas consideradas. Por ejemplo, si estamos hablando del desplazamiento de un vehículo sobre distancias de kilómetros a lo largo de minutos, un intervalo de milisegundos puede tratarse como un diferencial de tiempo, y un desplazamiento de milímetros puede considerarse un desplazamiento diferencial.

2.4 Trayectoria

Una partícula, al evolucionar en el tiempo, salvo cuando se encuentre en reposo, describe una curva en el espacio. Esta curva se conoce como la trayectoria de la partícula. Las ecuaciones horarias sirven como ecuaciones paramétricas de la trayectoria, siendo el tiempo el parámetro.

No obstante, a una misma trayectoria le pueden corresponder infinitas ecuaciones horarias, dependiendo del ritmo con el que se recorre la curva. Por ejemplo, las ecuaciones horarias

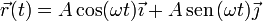
$\vec{r}(t) = A\cos(\omega t)\vec{\imath}+A\,\mathrm{sen}\,(\omega t)\vec{\jmath}$

y

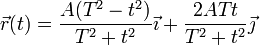
$\vec{r}(t) = \frac{A(T^2-t^2)}{T^2+t^2}\vec{\imath}+\frac{2ATt}{T^2+t^2}\vec{\jmath}$

corresponden a la misma trayectoria, una circunferencia horizontal.

En ocasiones, para indicar la trayectoria es preferible usar ecuaciones implícitas. En estas, se dan dos funciones (una sola, si el movimiento es plano), tales que

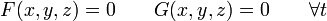
$F(x,y,z) = 0\qquad G(x,y,z) = 0\qquad \forall t$

Así, los dos ejemplos anteriores verifican

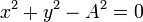
$x^2 + y^2 - A^2 = 0\,$ $z=0\,$

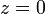
2.5 Parametrización natural

Para evitar el problema que supone identificar si las trayectorias de diferentes movimientos son coincidentes o no (debido a las diferencias en el ritmo con el que se recorre) se introduce la parametrización natural única para cada trayectoria (salvo un signo).

la idea es sencilla. En lugar de etiquetar cada punto de la trayectoria con el instante en que se pasa por él, se etiqueta usando la distancia $s$ a un punto de referencia:

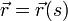
$\vec{r}=\vec{r}(s)$

Esto es exactamente lo que se hace en las carreteras, cuyos puntos se identifican mediante los postes kilométricos (y no por la hora en que un viajero concreto pase por cada punto).

La parametrización natural es única para cada trayectoria, salvo el signo correspondiente al sentido en que se recorre la curva (en el caso de la carretera, si desde Sevilla a Granada, o desde Granada a Sevilla). También el punto desde el que se empieza a contar queda libre.

A la variable $s$ , que mide la distancia sobre la curva se la denomina parámetro natural o parámetro arco. Para medir la distancia a lo largo de la curva lo que se hace es rectificar esta. Rectificar consiste en descomponer la curva en una infinitud de trozos de longitud diferencial, cada uno de los cuales se puede considerar aproximadamente rectilíneo, de forma que

$\mathrm{d}s=|\mathrm{d}\vec{r}|$

Sumando las longitudes de muchos trocitos diferenciales (esto es, integrando), obtenemos el valor del parámetro arco en un punto de la curva

$s = s_0+\int_{\vec{r}_0}^\vec{r} |\mathrm{d}\vec{r}|$

3 Velocidad

3.1 Velocidad media

3.2 Velocidad instantánea

4 Aceleración

5 Componentes intrínsecas

5.1 Velocidad

5.2 Aceleración

5.3 Triedro de Frenet

6 Ejemplos de movimientos

6.1 Rectilíneo

6.2 Parabólico

6.3 Circular

6.4 Helicoidal

6.5 Armónico simple

7 Problemas

@@ Línea 62: / Línea 62: @@
 La parametrización natural es única para cada trayectoria, salvo el signo correspondiente al sentido en que se recorre la curva (en el caso de la carretera, si desde Sevilla a Granada, o desde Granada a Sevilla). También el punto desde el que se empieza a contar queda libre.
-A la variable <math>s</math>, que mide la distancia sobre la curva se la denomina ''parámetro natural'' o ''parámetro arco''.
+A la variable <math>s</math>, que mide la distancia sobre la curva se la denomina ''parámetro natural'' o ''parámetro arco''. Para medir la distancia a lo largo de la curva lo que se hace es ''rectificar'' esta. Rectificar consiste en descomponer la curva en una infinitud de trozos de longitud diferencial, cada uno de los cuales se puede considerar aproximadamente rectilíneo, de forma que
+<center><math>\mathrm{d}s=|\mathrm{d}\vec{r}|</math></center>
+Sumando las longitudes de muchos trocitos diferenciales (esto es, integrando), obtenemos el valor del parámetro arco en un punto de la curva
+<center><math>s = s_0+\int_{\vec{r}_0}^\vec{r} |\mathrm{d}\vec{r}|</math></center>
 ==Velocidad==