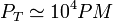Potencia radiada por el Sol
De Laplace
(Nueva página: == Enunciado == La superficie del Sol tiene una temperatura de unos 5800 K. El radio del Sol es igual a <math>6.96\times10^8\,\mathrm{m}</math>. Calcule la energía total radiada por...) |
(→Solución) |
||
| (3 ediciones intermedias no se muestran.) | |||
| Línea 10: | Línea 10: | ||
<center> | <center> | ||
<math> | <math> | ||
| - | P=\sigma A e T^4 | + | P=\sigma A e T^4\, |
</math> | </math> | ||
</center> | </center> | ||
| Línea 43: | Línea 43: | ||
</math> | </math> | ||
</center> | </center> | ||
| - | No aparece el factor 4 porque el Sol ve a la Tierra esencialmente como un disco plano de radio <math>R_T</math>. Así, pues la potencia recibida | + | No aparece el factor 4 porque el Sol ve a la Tierra esencialmente como un disco plano de radio <math>R_T</math>. Así, pues la potencia recibida por la superficie de la Tierra es |
| - | por la superficie de la Tierra es | + | |
<center> | <center> | ||
<math> | <math> | ||
| Línea 50: | Línea 49: | ||
</math> | </math> | ||
</center> | </center> | ||
| - | Podemos comparar esta potencia con el consumo energético medio mundial. En el año | + | Podemos comparar esta potencia con el consumo energético medio mundial. En el año 2008 este consumo fue |
| + | <math>CEM\simeq 5\times10^{20}\,\mathrm{J}</math>, que corresponde a una potencia media de consumo | ||
<math> | <math> | ||
| - | + | PM=1.5\times10^{13}\,\mathrm{W} | |
</math>. | </math>. | ||
Por tanto, la potencia que recibe la Tierra es | Por tanto, la potencia que recibe la Tierra es | ||
<center> | <center> | ||
<math> | <math> | ||
| - | P_T\simeq10^ | + | P_T\simeq10^4PM |
</math> | </math> | ||
</center> | </center> | ||
| + | |||
| + | [[Categoría:Problemas del primer principio de la termodinámica]] | ||
última version al 17:54 13 may 2010
1 Enunciado
La superficie del Sol tiene una temperatura de unos 5800 K. El radio del Sol es igual a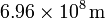 
.
Calcule la energía total radiada por el Sol cada segundo si la emisividad es e = 0.965. Calcule la potencia que llega a la superficie
de la Tierra, si el radio de esta es 
, y la distancia media Tierra-Sol es
.
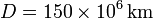2 Solución
La potencia emitida por una superficie irradiante es
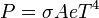
donde T es la temperatura absoluta,e es la emisividad de la superficie, A es el área de la superficie
emisora y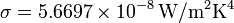 
es la constante de Stefan-Boltzmann.
En nuestro caso la superficie emisora es la del Sol. A partir de su radio podemos calcularla
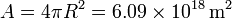
Con los dos datos del problema podemos calcular la potencia radiada por el Sol
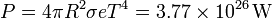
Para calcular la fracción de esta potencia recibida por la Tierra, consideramos la esfera con centro en el Sol y de radio la distancia media entre el Sol y la Tierra. La superficie de esta esfera es
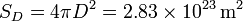
La potencia total emitida por el Sol se distribuye uniformemente sobre esta superficie. La fracción de esta potencia recibida por el Sol es igual a la fracción de la superficie que la Tierra ofrece al Sol respecto a SD. Esta fracción es
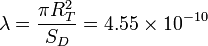
No aparece el factor 4 porque el Sol ve a la Tierra esencialmente como un disco plano de radio RT. Así, pues la potencia recibida por la superficie de la Tierra es
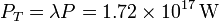
Podemos comparar esta potencia con el consumo energético medio mundial. En el año 2008 este consumo fue
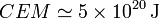, que corresponde a una potencia media de consumo
.
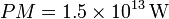Por tanto, la potencia que recibe la Tierra es
