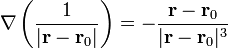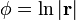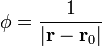Regla de la cadena para gradientes
De Laplace
(→Primer caso) |
(→Demostración) |
||
| (9 ediciones intermedias no se muestran.) | |||
| Línea 12: | Línea 12: | ||
==Solución== | ==Solución== | ||
===Demostración=== | ===Demostración=== | ||
| - | + | Para demostrar esto, recordamos que el gradiente se define como el único vector que, sea cual sea la dirección tomada, la [[derivada direccional]] puede calcularse como | |
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | <center><math>\frac{\partial \phi}{\partial v} = \nabla\phi\cdot\mathbf{v}</math></center> | |
| - | + | Por la definición de derivada direccional tenemos que | |
| - | + | <center><math>\frac{\partial \phi}{\partial v} = \frac{\mathrm{d}\phi}{|\mathrm{d}\mathbf{r}|}</math></center> | |
| - | \mathrm{d}\phi=\frac{\mathrm{d}\phi}{\mathrm{d}u}\,\mathrm{d}u=\frac{\mathrm{d}\phi}{\mathrm{d}u}\,\nabla | + | siendo <math>|\mathrm{d}\mathbf{r}|</math> un desplazamiento infinitesimal en la dirección de <math>\mathbf{v}</math>. Si en la expresión anterior multiplicamos y dividimos por <math>\mathrm{d}u</math>, el incremento en u cuando realizamos dicho desplazamiento, queda |
| - | u | + | |
| - | + | <center><math>\frac{\partial \phi}{\partial v} = \frac{\mathrm{d}\phi}{\mathrm{d}u}\,\frac{\mathrm{d}u}{|\mathrm{d}\mathbf{r}|}</math></center> | |
| - | + | ||
| + | El primer factor es la derivada de <math>\phi\,</math> respecto a <math>u</math>, mientras que el segundo es la derivada direccional de <math>u</math> en la dirección de <math>\mathbf{v}</math>, por tanto | ||
| + | |||
| + | <center><math>\frac{\partial \phi}{\partial v} = \frac{\mathrm{d}\phi}{\mathrm{d}u}\,\nabla u\cdot\mathbf{v}= \left(\frac{\mathrm{d}\phi}{\mathrm{d}u}\,\nabla u\right)\cdot\mathbf{v} </math></center> | ||
| + | |||
| + | pero puesto que <math>\nabla\phi</math> es el único vector que al multiplicarlo por <math>\mathbf{v}</math> nos da la derivada direccional de <math>\phi\,</math> se llega a la conclusión de que | ||
| + | |||
| + | <center><math>\nabla\phi = \frac{\mathrm{d}\phi}{\mathrm{d}u}\nabla u</math></center> | ||
===Primer caso=== | ===Primer caso=== | ||
| Línea 50: | Línea 51: | ||
por lo que, igualando las dos expresiones, | por lo que, igualando las dos expresiones, | ||
| - | <center><math>2r\nabla r=2\mathbf{r}</math>{{tose}}\nabla r=\frac{\mathbf{r}}{r}</center> | + | <center><math>2r\nabla r=2\mathbf{r}</math>{{tose}}<math>\nabla r=\frac{\mathbf{r}}{r}</math></center> |
y, para cualquier potencia de <math>r</math> | y, para cualquier potencia de <math>r</math> | ||
| Línea 68: | Línea 69: | ||
Para el caso de una función que depende exclusivamente de la distancia al origen (un campo central), el gradiente se reduce a | Para el caso de una función que depende exclusivamente de la distancia al origen (un campo central), el gradiente se reduce a | ||
| - | <math>\nabla\phi(r) = \frac{\mathrm{d}\phi}{\mathrm{d}r}\mathbf{u}_{r}</math> | + | <center><math>\nabla\phi(r) = \frac{\mathrm{d}\phi}{\mathrm{d}r}\mathbf{u}_{r}</math></center> |
que para <math>\phi=r^n\,</math> da | que para <math>\phi=r^n\,</math> da | ||
| Línea 74: | Línea 75: | ||
<center><math>\nabla(r^n)= n r^{n-1} \mathbf{u}_{r} = n r^{n-2}\mathbf{r}</math></center> | <center><math>\nabla(r^n)= n r^{n-1} \mathbf{u}_{r} = n r^{n-2}\mathbf{r}</math></center> | ||
| - | y para <math>\phi=\ln(r)</math> | + | y para <math>\phi=\ln(r)\,</math> |
<center><math>\nabla(\ln(r)) = \frac{1}{r}\mathbf{u}_{r} = \frac{\mathbf{r}}{r^2}</math></center> | <center><math>\nabla(\ln(r)) = \frac{1}{r}\mathbf{u}_{r} = \frac{\mathbf{r}}{r^2}</math></center> | ||
| Línea 82: | Línea 83: | ||
<center><math>\nabla |\mathbf{r}-\mathbf{r}_0|^n=n|\mathbf{r}-\mathbf{r}_0|^{n-1}\nabla|\mathbf{r}-\mathbf{r}_0|</math></center> | <center><math>\nabla |\mathbf{r}-\mathbf{r}_0|^n=n|\mathbf{r}-\mathbf{r}_0|^{n-1}\nabla|\mathbf{r}-\mathbf{r}_0|</math></center> | ||
| + | |||
<center><math>\nabla|\mathbf{r}-\mathbf{r}_0|^2=\nabla\left(\left(\mathbf{r}-\mathbf{r}_0\right){\cdot}\left(\mathbf{r}-\mathbf{r}_0\right)\right) | <center><math>\nabla|\mathbf{r}-\mathbf{r}_0|^2=\nabla\left(\left(\mathbf{r}-\mathbf{r}_0\right){\cdot}\left(\mathbf{r}-\mathbf{r}_0\right)\right) | ||
| Línea 88: | Línea 90: | ||
El gradiente del primer término es conocido | El gradiente del primer término es conocido | ||
| - | <math>\nabla(r^2) = 2\mathbf{r}</math> | + | <center><math>\nabla(r^2) = 2\mathbf{r}</math></center> |
| - | El segundo, de acuerdo con lo que se demuestra en un problema de [[identidades vectoriales]] | + | El segundo, de acuerdo con lo que se demuestra en un problema de [[Demostración de identidades vectoriales|identidades vectoriales]] |
<center><math>\nabla(2\mathbf{r}{\cdot}\mathbf{r}_0) = 2\mathbf{r}_0</math></center> | <center><math>\nabla(2\mathbf{r}{\cdot}\mathbf{r}_0) = 2\mathbf{r}_0</math></center> | ||
última version al 20:15 13 abr 2010
Contenido |
1 Enunciado
Si 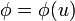 , con
, con 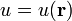 , demuestre que
, demuestre que
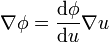
Encuentre 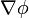 si
si
2 Solución
2.1 Demostración
Para demostrar esto, recordamos que el gradiente se define como el único vector que, sea cual sea la dirección tomada, la derivada direccional puede calcularse como
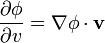
Por la definición de derivada direccional tenemos que

siendo 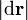 un desplazamiento infinitesimal en la dirección de
un desplazamiento infinitesimal en la dirección de  . Si en la expresión anterior multiplicamos y dividimos por du, el incremento en u cuando realizamos dicho desplazamiento, queda
. Si en la expresión anterior multiplicamos y dividimos por du, el incremento en u cuando realizamos dicho desplazamiento, queda
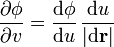
El primer factor es la derivada de  respecto a u, mientras que el segundo es la derivada direccional de u en la dirección de
respecto a u, mientras que el segundo es la derivada direccional de u en la dirección de  , por tanto
, por tanto
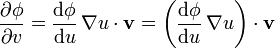
pero puesto que 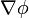 es el único vector que al multiplicarlo por
es el único vector que al multiplicarlo por  nos da la derivada direccional de
nos da la derivada direccional de  se llega a la conclusión de que
se llega a la conclusión de que
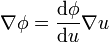
2.2 Primer caso
Empleando este teorema es posible calcular multitud de gradientes. Así los correspondientes a los apartados 1 y 2 se pueden obtener a partir del de la función u = r.
Para cualquier potencia de r se tendrá

por lo que el problema se reduce a calcular 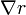 . Si aplicamos la fórmula anterior a r2 queda
. Si aplicamos la fórmula anterior a r2 queda
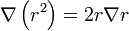
pero
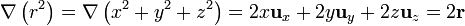
por lo que, igualando las dos expresiones,
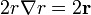


y, para cualquier potencia de r
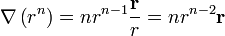
2.3 Segundo caso
Para el caso del logaritmo se tiene
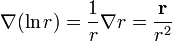
Un método alternativo para estos dos casos es empleando coordenadas esféricas
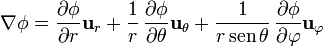
Para el caso de una función que depende exclusivamente de la distancia al origen (un campo central), el gradiente se reduce a
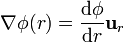
que para 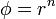 da
da
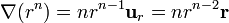
y para 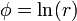
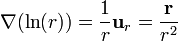
2.4 Tercer caso
Para la última función efectuamos un cálculo análogo, notando que
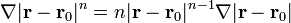

El gradiente del primer término es conocido
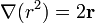
El segundo, de acuerdo con lo que se demuestra en un problema de identidades vectoriales

El tercer sumando se anula, por ser un vector constante
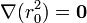
Reuniendo los tres términos
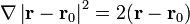
y de aquí
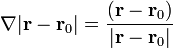

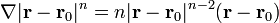
y, en particular