Líneas y superficies coordenadas
De Laplace
(Nueva página: ==Introducción== ¿Por qué se definen diferentes sistemas de coordenadas? ¿Por qué no basta con las coordenadas cartesianas? La respuesta, evidente a partir de ejemplos sencillos...) |
|||
| Línea 1: | Línea 1: | ||
==Introducción== | ==Introducción== | ||
| - | ¿Por qué se definen diferentes sistemas de coordenadas? ¿Por qué no basta con las coordenadas cartesianas? La respuesta, evidente a partir de ejemplos sencillos, es que unos sistemas son más adecuados que otros dependiendo del problema a resolver. | + | ¿Por qué se definen diferentes sistemas de coordenadas? ¿Por qué no basta con las coordenadas cartesianas? La respuesta, evidente a partir de ejemplos sencillos, es que unos sistemas son más adecuados que otros dependiendo del problema a resolver. Simplifican los cálculos y permiten una interpretación sencilla de los resultados obtenidos. |
Ahora bien, ¿cuál es el factor principal para elegir un sistema u otro? A la vista de un problema concreto, ¿cómo sabemos si debemos resolverlo empleando coordenadas cartesianas, cilíndricas o esféricas? | Ahora bien, ¿cuál es el factor principal para elegir un sistema u otro? A la vista de un problema concreto, ¿cómo sabemos si debemos resolverlo empleando coordenadas cartesianas, cilíndricas o esféricas? | ||
| Línea 8: | Línea 8: | ||
Por ejemplo, si tenemos una distribución de carga en forma de esfera, parece natural elegir coordenadas esféricas. Si tenemos un hilo rectilíneo cargado, tanto cartesianas como cilíndricas parecen adecuadas. Pero, ¿qué hacemos si tenemos una superficie cónica? Para poder decidir, es necesario visualizar correctamente los diferentes sistemas de coordenadas. Esto se consigue con ayuda de las líneas y superficies coordenadas. | Por ejemplo, si tenemos una distribución de carga en forma de esfera, parece natural elegir coordenadas esféricas. Si tenemos un hilo rectilíneo cargado, tanto cartesianas como cilíndricas parecen adecuadas. Pero, ¿qué hacemos si tenemos una superficie cónica? Para poder decidir, es necesario visualizar correctamente los diferentes sistemas de coordenadas. Esto se consigue con ayuda de las líneas y superficies coordenadas. | ||
| - | Líneas coordenadas | + | ==Líneas coordenadas == |
| - | Un punto P del espacio viene dado por tres valores ( | + | Un punto P del espacio viene dado por tres valores <math>(q_{10}, q_{20}, q_{30})\,</math>. Si, partiendo de este punto, modificamos el valor de la coordenada <math>q_1\,</math>, manteniendo fijas las otras dos, obtenemos una curva (función de <math>q_1\,</math>) conocida como línea coordenada <math>q_1\,</math>. Del mismo modo, si variamos <math>q_2\,</math> o <math>q_3\,</math>, manteniendo en cada caso fijas las otras dos coordenadas, obtenemos otras dos líneas coordenadas (<math>q_2\,</math> y <math>q_3\,</math>, respectivamente). |
De aquí se deduce que, por cada punto del espacio pasan tres líneas coordenadas. | De aquí se deduce que, por cada punto del espacio pasan tres líneas coordenadas. | ||
| - | Superficies coordenadas | + | ==Superficies coordenadas== |
| - | Si dado un punto P identificado por las coordenadas ( | + | Si dado un punto P identificado por las coordenadas <math>(q_{10}, q_{20}, q_{30})\,</math> variamos dos de ellas, <math>q_1\,</math> y <math>q_2\,</math> manteniendo fija la tercera, nos movemos sobre una superficie. Ésta se denomina superficie coordenada <math>q_3 = \mathrm{cte}</math>. Análogamente se tienen las superficies coordenadas <math>q_1 = \mathrm{cte}</math> y <math>q_2 = \mathrm{cte}</math>. |
De esta definición se deduce que | De esta definición se deduce que | ||
| - | Por cada punto P pasan tres superficies coordenadas. | + | Por cada punto <math>P</math> pasan tres superficies coordenadas. |
La intersección de dos superficies coordenadas es una línea coordenada (Ejercicio: demostrarlo). | La intersección de dos superficies coordenadas es una línea coordenada (Ejercicio: demostrarlo). | ||
Revisión de 19:00 19 nov 2007
1 Introducción
¿Por qué se definen diferentes sistemas de coordenadas? ¿Por qué no basta con las coordenadas cartesianas? La respuesta, evidente a partir de ejemplos sencillos, es que unos sistemas son más adecuados que otros dependiendo del problema a resolver. Simplifican los cálculos y permiten una interpretación sencilla de los resultados obtenidos.
Ahora bien, ¿cuál es el factor principal para elegir un sistema u otro? A la vista de un problema concreto, ¿cómo sabemos si debemos resolverlo empleando coordenadas cartesianas, cilíndricas o esféricas?
La respuesta es que la elección depende de la geometría del sistema. En particular, son las líneas y superficies que aparecen las que nos inclinan por una elección concreta (que a veces puede resultar infructuosa).
Por ejemplo, si tenemos una distribución de carga en forma de esfera, parece natural elegir coordenadas esféricas. Si tenemos un hilo rectilíneo cargado, tanto cartesianas como cilíndricas parecen adecuadas. Pero, ¿qué hacemos si tenemos una superficie cónica? Para poder decidir, es necesario visualizar correctamente los diferentes sistemas de coordenadas. Esto se consigue con ayuda de las líneas y superficies coordenadas.
2 Líneas coordenadas
Un punto P del espacio viene dado por tres valores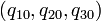 
. Si, partiendo de este punto, modificamos el valor de la coordenada 
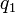, manteniendo fijas las otras dos, obtenemos una curva (función de 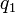) conocida como línea coordenada 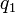. Del mismo modo, si variamos 
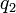o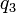 
, manteniendo en cada caso fijas las otras dos coordenadas, obtenemos otras dos líneas coordenadas ( 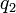y 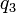, respectivamente).
De aquí se deduce que, por cada punto del espacio pasan tres líneas coordenadas.
3 Superficies coordenadas
Si dado un punto P identificado por las coordenadas 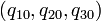variamos dos de ellas, 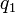y 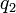manteniendo fija la tercera, nos movemos sobre una superficie. Ésta se denomina superficie coordenada q3 = cte. Análogamente se tienen las superficies coordenadas q1 = cte y q2 = cte.
De esta definición se deduce que
Por cada punto P pasan tres superficies coordenadas.
La intersección de dos superficies coordenadas es una línea coordenada (Ejercicio: demostrarlo).
