Espira cuadrada rotatoria en un campo magnético
De Laplace
(Diferencias entre revisiones)
(→Cálculo de la intensidad) |
(→Cálculo de la intensidad) |
||
| Línea 17: | Línea 17: | ||
por ser <math>\mathbf{B}_0</math> uniforme. El producto escalar es igual al producto de los módulos por el coseno del ángulo que forman, el cual varía uniformemente con el tiempo | por ser <math>\mathbf{B}_0</math> uniforme. El producto escalar es igual al producto de los módulos por el coseno del ángulo que forman, el cual varía uniformemente con el tiempo | ||
| - | <center><math>\Phi_m=B_0a^2\cos(\omega t)</math></center> | + | <center><math>\Phi_m=B_0a^2\cos(\omega t)\,</math></center> |
Derivando obtenemos la fuerza electromotriz. | Derivando obtenemos la fuerza electromotriz. | ||
| Línea 28: | Línea 28: | ||
| - | <center><math>\mathcal{E}_0=0. | + | <center><math>\mathcal{E}_0=0.20\,\mathrm{V}</math></center> |
La corriente que circula por la espira es igual a | La corriente que circula por la espira es igual a | ||
| - | <math>I=\frac{\mathcal{E}}{R}=\frac{B_0a^2\omega}{R}\mathrm{sen}(\omega t)</math> | + | <center><math>I=\frac{\mathcal{E}}{R}=\frac{B_0a^2\omega}{R}\mathrm{sen}(\omega t)</math></center> |
donde la resistencia vale | donde la resistencia vale | ||
| - | <center><math>R=\frac{4a}{\sigma A} = </math></center> | + | <center><math>R=\frac{4a}{\sigma A} = 2.7\,\mathrm{m}\Omega</math></center> |
| + | |||
| + | y la amplitud de la intensidad | ||
| + | |||
| + | <center><math>I_0=\frac{\mathcal{E}_0}{R}=\frac{B_0aA\sigma\omega}{4} = 74\,\mathrm{A}</math></center> | ||
===Cálculo de la potencia=== | ===Cálculo de la potencia=== | ||
[[Categoría:Problemas de inducción electromagnética]] | [[Categoría:Problemas de inducción electromagnética]] | ||
Revisión de 08:48 24 may 2008
Contenido |
1 Enunciado
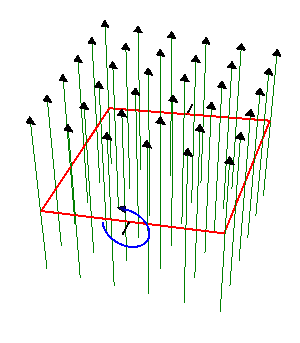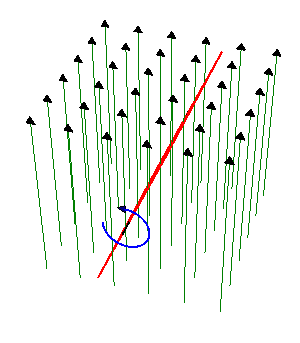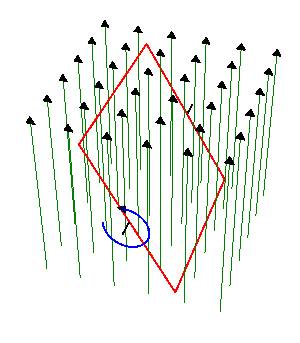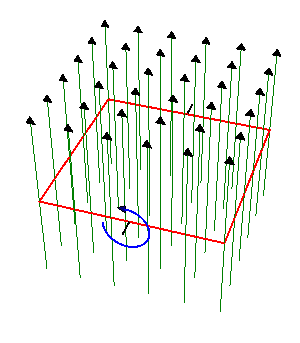
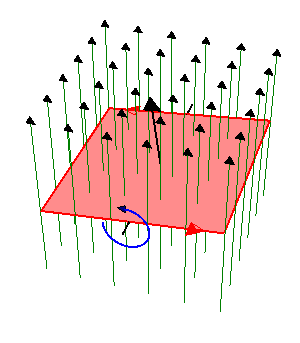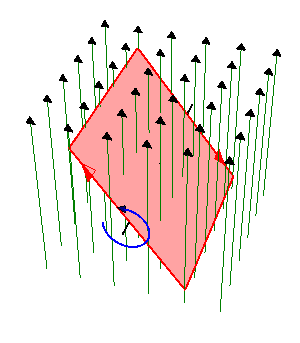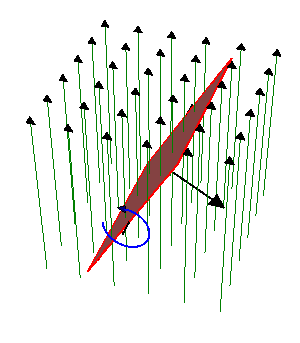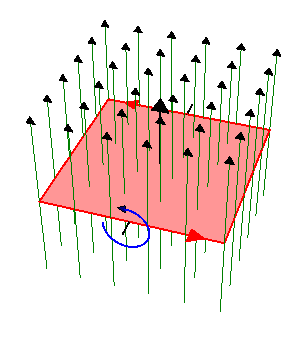
Una espira cuadrada de lado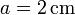 , de hilo de cobre de sección
, de hilo de cobre de sección 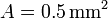 gira con frecuencia
gira con frecuencia 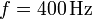 en el interior de un campo magnético uniforme de módulo
en el interior de un campo magnético uniforme de módulo 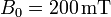 . El eje de giro es perpendicular al campo magnético.
. El eje de giro es perpendicular al campo magnético.
- Determine la corriente que se induce en la espira.
- Calcule la potencia instantánea disipada en la espira y la energía total disipada en un periodo de giro.
2 Solución
2.1 Cálculo de la intensidad
Éste es un ejemplo elemental de generador de corriente alterna. La corriente se obtiene por aplicación directa de la ley de Faraday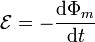
El flujo magnético es igual a
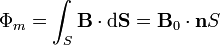
por ser  uniforme. El producto escalar es igual al producto de los módulos por el coseno del ángulo que forman, el cual varía uniformemente con el tiempo
uniforme. El producto escalar es igual al producto de los módulos por el coseno del ángulo que forman, el cual varía uniformemente con el tiempo
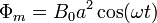
Derivando obtenemos la fuerza electromotriz.
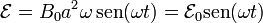
Vemos que este sistema se comporta como un generador de corriente alterna. Sustituyendo los valores numéricos
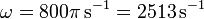
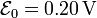
La corriente que circula por la espira es igual a
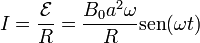
donde la resistencia vale
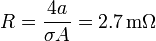
y la amplitud de la intensidad