Incertidumbre de una magnitud función de otra(s)
De Laplace
(Nueva página: __TOC__ Cuando se tienen una o varias medidas directas de una magnitud, es inmediato dar expresiones para la incertidumbre en las medidas. En muchos casos, no obstante, debemos traba...) |
(→Función de una sola variable) |
||
| (7 ediciones intermedias no se muestran.) | |||
| Línea 3: | Línea 3: | ||
En muchos casos, no obstante, debemos trabajar con cantidades indirectas, obtenidas a partir de las medidas. Estas pueden depender de | En muchos casos, no obstante, debemos trabajar con cantidades indirectas, obtenidas a partir de las medidas. Estas pueden depender de | ||
| - | una sola variable experimental <math>z= f(x</math> o de varias magnitudes diferentes <math>z = f(x,y,\dots)</math>. | + | una sola variable experimental <math>z= f(x)</math> o de varias magnitudes diferentes <math>z = f(x,y,\dots)</math>. |
==Función de una sola variable== | ==Función de una sola variable== | ||
| + | A modo de ejemplo, supongamos que, dado el diámetro <math>D_0=12.5\pm 0.3\,\mathrm{cm}</math> de un cable, debemos determinar el área de su sección, de la que sabemos que es circular. El cálculo de la sección es inmediato | ||
| + | |||
| + | <center><math>A = \frac{\pi D_0^2}{4}=122.718\,\mathrm{cm}^2</math></center> | ||
| + | |||
| + | pero si el diámetro es una cantidad con una cierta incertidumbre, medida por su banda de error, ¿cuál es la banda de error del área? | ||
| + | |||
| + | Podemos hacer una primera estimación. Supongamos que <math>E_D</math> es el error del diámetro, de forma que hay un 95% de probabilidad de que <math>D</math> se encuentre en el intervalo | ||
| + | |||
| + | <center><math>D\in (D_0-E_D, D_0+ E_D) = (12.2\,\mathrm{cm},12.8\,\mathrm{cm})</math></center> | ||
| + | |||
| + | de forma que el área posee un 95% de probabilidad de encontrarse en el intervalo | ||
| + | |||
| + | <center><math>A\in\left(\frac{\pi(D_0-E_D)^2}{4},\frac{\pi(D_0+E_D)^2}{4}\right)=\left(116.899\,\mathrm{cm}^2,128.680\,\mathrm{cm}^2\right)</math></center> | ||
| + | |||
| + | Esta estimación, aun siendo correcta, tiene el inconveniente de que proporciona una banda de error asimétrica, ya que el valor de <math>A</math> indicado antes no se encuentra en el punto medio de este intervalo (que se halla en 122.789 cm²). O, equivalentemente, que el punto medio del intervalo no es la mejor aproximación para el área. | ||
| + | |||
| + | Podemos simplificar las fórmulas en el caso de que el error <math>E_x</math> sea mucho menor que la propia cantidad <math>x</math> (lo que ocurre a menudo, pero no siempre). En este caso, tal como se detalla en [[Deducción_de_las_fórmulas_para_la_incertidumbre#Error_de_una_funci.C3.B3n|otro artículo]] resulta, en primer orden | ||
| + | |||
| + | <center><math>E_f = \left|\frac{\mathrm{d}f}{\mathrm{d}x}\right| E_x</math></center> | ||
| + | |||
| + | de forma que la cantidad derivada se expresará como | ||
| + | |||
| + | <center><math>f = f(x) \pm \left|\frac{\mathrm{d}f}{\mathrm{d}x}\right| E_x</math></center> | ||
| + | |||
| + | El valor absoluto de la derivada se debe a que debemos obtener siempre un error positivo de la magnitud. | ||
| + | |||
| + | Así, para el caso del área, tendremos | ||
| + | |||
| + | <center><math>\frac{\mathrm{d}A}{\mathrm{d}D} = \frac{\pi D}{2} \qquad A = \frac{\pi D^2}{4}\pm \frac{\pi D E_D}{2} = 122.718\pm | ||
| + | 5.890\,\mathrm{cm}^2 = 123\pm 6 \,\mathrm{cm}^2</math></center> | ||
| + | |||
| + | Puede comprobarse que esto es lo que resulta en el intervalo que hallamos antes si suponemos <math>E_D\ll D</math>. | ||
| + | |||
| + | De esta fórmula hay varios casos particulares de interés | ||
| + | |||
| + | ;Proporcionalidad: Para una variable proporcional a otra | ||
| + | |||
| + | <center><math>y = K x\,</math></center> | ||
| + | |||
| + | :con <math>K</math> una constante ''sin error'' (por ejemplo, 2 ó π) | ||
| + | |||
| + | <center><math>E_y = K E_x\,</math></center> | ||
| + | |||
| + | ;Exponencial: Para la función exponencial | ||
| + | |||
| + | <center><math>y = a \mathrm{e}^{x}\,</math></center> | ||
| + | |||
| + | :resulta | ||
| + | |||
| + | <center><math>E_y = a \mathrm{e}^{x} E_x = y E_x\,</math></center> | ||
| + | |||
| + | :o, lo que es equivalente | ||
| + | |||
| + | <center><math>\epsilon_y = \frac{E_y}{y} = E_x</math></center> | ||
| + | |||
| + | : esto es, el error relativo de $y$ coincide con el error absoluto de <math>x</math>. | ||
| + | |||
| + | ;Logaritmo: Para el logaritmo tenemos la relación inversa | ||
| + | |||
| + | <center><math>y = \ln(x)\,</math>{{tose}}<math>E_y = \frac{E_x}{x} = \epsilon_x</math></center> | ||
| + | |||
| + | :El error absoluto de <math>y</math> coincide con el relativo de <math>x</math>. | ||
| + | |||
| + | ==Función de varias variables== | ||
| + | Supongamos ahora que debemos hallar el volumen de un recipiente cilíndrico, del cual hemos medido por separado el diámetro de la base y la altura, con valores | ||
| + | |||
| + | <center><math>D = 12.5\pm 0.1 \,\mathrm{cm} \qquad h = 10.2\pm 0.2\,\mathrm{cm}</math></center> | ||
| + | |||
| + | El volumen valdrá | ||
| + | |||
| + | <center><math>V = \frac{\pi D^2 h}{4} \sim 1251.7\,\mathrm{cm}^3</math></center> | ||
| + | |||
| + | Para hallar el error de esta cantidad debemos tener en cuenta que tanto <math>D</math> como <math>h</math> están sujetos a error, por lo que el error de <math>V</math> es una combinación de ambos. | ||
| + | |||
| + | Dada una función <math>z=f(x,y,\dots)</math>, la fórmula para el error de <math>z</math> en el caso de que <math>x</math>, <math>y</math>,… sean variables independientes (esto es, que la medida de una no afecta a la medida de la otra) es una generalización del caso de una sola variable | ||
| + | |||
| + | <center><math>E_z = \sqrt{\left(\frac{\partial z}{\partial x}\right)^2E_x^2+\left(\frac{\partial z}{\partial y}\right)^2E_y^2+\ldots}</math></center> | ||
| + | |||
| + | Podemos ver como para el caso de una sola variable la expresión se reduce a la que ya conocemos. | ||
| + | |||
| + | Así para el caso del volumen tendríamos | ||
| + | |||
| + | <center><math>\frac{\partial V}{\partial D} = \frac{\pi D h}{2} = 200.3\,\mathrm{cm}^2\qquad\frac{\partial V}{\partial h} = \frac{\pi D^2}{4} = 122.7\,\mathrm{cm}^2</math>{{qquad}}{{qquad}} | ||
| + | <math>E_V = \sqrt{200.3^2\times 0.1^2 + 122.7^2\times 0.2^2}\,\mathrm{cm}^3= 31.7\,\mathrm{cm}^3</math></center> | ||
| + | |||
| + | y la expresión final del volumen es | ||
| + | |||
| + | <center><math>V = 1250\pm 30\,\mathrm{cm}^3</math></center> | ||
| + | |||
| + | Una comparación interesante es la del error relativo de las tres cantidades | ||
| + | |||
| + | <center><math>\epsilon_D = 0.8\% \qquad \epsilon_h = 2.0\%\qquad \epsilon_V = 2.4\%</math></center> | ||
| + | |||
| + | Como indicación de si un resultado puede ser correcto, podemos observar que el error relativo del resultado final debe ser algo mayor que el mayor de los errores relativos individuales. Si resulta un error relativo mucho menor es que algo falla. | ||
| + | |||
| + | Como casos particulares de la fórmula del error de una función tenemos los siguientes. | ||
| + | |||
| + | ;Suma de variables: Si tenemos una función de la forma | ||
| + | |||
| + | <center><math>u = x\pm y \pm z \pm \cdots</math></center> | ||
| + | |||
| + | :esto es, formada exclusivamente por sumas o restas, el error absoluto de <math>u</math> vale | ||
| + | |||
| + | <center><math>E_u = \sqrt{E_x^2+E_y^2+E_z^2 + \cdots}</math></center> | ||
| + | |||
| + | :es decir, la suma cuadrática de los errores individuales. | ||
| + | ;Producto de variables: Para una función del tipo | ||
| + | |||
| + | <center><math>u = \frac{x{\cdot}y{\cdot}\cdots}{z{\cdot}t{\cdot}\cdots}</math></center> | ||
| + | |||
| + | :formada solamente por productos y cocientes (pero ninguna suma o resta) operando en la expresión del error se llega a | ||
| + | |||
| + | <center><math>\epsilon_u = \sqrt{\epsilon_x^2+\epsilon_y^2+\epsilon_z^2 + \cdots}</math></center> | ||
| + | |||
| + | :esto es, el error ''relativo'' de <math>u</math> es la suma cuadrática de los errores ''relativos'' individuales. Es decir, para hallar el error absoluto de <math>u</math> (que es el que acompaña a la medida) de esta forma habría que calcular previamente los errores relativos de cada factor, computar el error relativo del producto y, multiplicando por la propia cantidad <math>u</math> llegaríamos a <math>E_u</math>, error absoluto de <math>u</math>. | ||
| + | |||
| + | [[Categoría:Prácticas de laboratorio]] | ||
última version al 18:51 19 mar 2010
Contenido |
Cuando se tienen una o varias medidas directas de una magnitud, es inmediato dar expresiones para la incertidumbre en las medidas.
En muchos casos, no obstante, debemos trabajar con cantidades indirectas, obtenidas a partir de las medidas. Estas pueden depender de
una sola variable experimental z = f(x) o de varias magnitudes diferentes 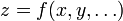 .
.
1 Función de una sola variable
A modo de ejemplo, supongamos que, dado el diámetro 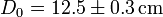 de un cable, debemos determinar el área de su sección, de la que sabemos que es circular. El cálculo de la sección es inmediato
de un cable, debemos determinar el área de su sección, de la que sabemos que es circular. El cálculo de la sección es inmediato
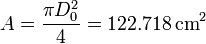
pero si el diámetro es una cantidad con una cierta incertidumbre, medida por su banda de error, ¿cuál es la banda de error del área?
Podemos hacer una primera estimación. Supongamos que ED es el error del diámetro, de forma que hay un 95% de probabilidad de que D se encuentre en el intervalo
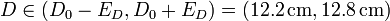
de forma que el área posee un 95% de probabilidad de encontrarse en el intervalo
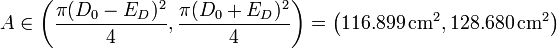
Esta estimación, aun siendo correcta, tiene el inconveniente de que proporciona una banda de error asimétrica, ya que el valor de A indicado antes no se encuentra en el punto medio de este intervalo (que se halla en 122.789 cm²). O, equivalentemente, que el punto medio del intervalo no es la mejor aproximación para el área.
Podemos simplificar las fórmulas en el caso de que el error Ex sea mucho menor que la propia cantidad x (lo que ocurre a menudo, pero no siempre). En este caso, tal como se detalla en otro artículo resulta, en primer orden
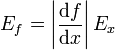
de forma que la cantidad derivada se expresará como
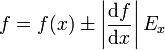
El valor absoluto de la derivada se debe a que debemos obtener siempre un error positivo de la magnitud.
Así, para el caso del área, tendremos
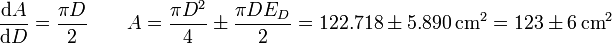
Puede comprobarse que esto es lo que resulta en el intervalo que hallamos antes si suponemos 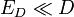 .
.
De esta fórmula hay varios casos particulares de interés
- Proporcionalidad
- Para una variable proporcional a otra
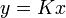
- con K una constante sin error (por ejemplo, 2 ó π)
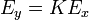
- Exponencial
- Para la función exponencial
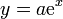
- resulta
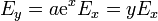
- o, lo que es equivalente
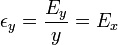
- esto es, el error relativo de $y$ coincide con el error absoluto de x.
- Logaritmo
- Para el logaritmo tenemos la relación inversa
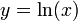

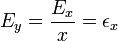
- El error absoluto de y coincide con el relativo de x.
2 Función de varias variables
Supongamos ahora que debemos hallar el volumen de un recipiente cilíndrico, del cual hemos medido por separado el diámetro de la base y la altura, con valores

El volumen valdrá
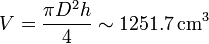
Para hallar el error de esta cantidad debemos tener en cuenta que tanto D como h están sujetos a error, por lo que el error de V es una combinación de ambos.
Dada una función 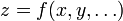 , la fórmula para el error de z en el caso de que x, y,… sean variables independientes (esto es, que la medida de una no afecta a la medida de la otra) es una generalización del caso de una sola variable
, la fórmula para el error de z en el caso de que x, y,… sean variables independientes (esto es, que la medida de una no afecta a la medida de la otra) es una generalización del caso de una sola variable
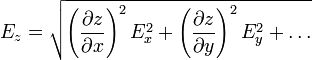
Podemos ver como para el caso de una sola variable la expresión se reduce a la que ya conocemos.
Así para el caso del volumen tendríamos
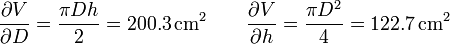
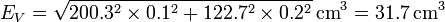
y la expresión final del volumen es
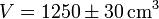
Una comparación interesante es la del error relativo de las tres cantidades
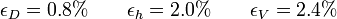
Como indicación de si un resultado puede ser correcto, podemos observar que el error relativo del resultado final debe ser algo mayor que el mayor de los errores relativos individuales. Si resulta un error relativo mucho menor es que algo falla.
Como casos particulares de la fórmula del error de una función tenemos los siguientes.
- Suma de variables
- Si tenemos una función de la forma
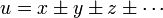
- esto es, formada exclusivamente por sumas o restas, el error absoluto de u vale
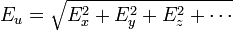
- es decir, la suma cuadrática de los errores individuales.
- Producto de variables
- Para una función del tipo
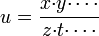
- formada solamente por productos y cocientes (pero ninguna suma o resta) operando en la expresión del error se llega a
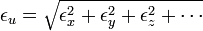
- esto es, el error relativo de u es la suma cuadrática de los errores relativos individuales. Es decir, para hallar el error absoluto de u (que es el que acompaña a la medida) de esta forma habría que calcular previamente los errores relativos de cada factor, computar el error relativo del producto y, multiplicando por la propia cantidad u llegaríamos a Eu, error absoluto de u.





