Incertidumbre en los datos
De Laplace
(Nueva página: ==Introducción== En Ingeniería y en las Ciencias Experimentales, a diferencia de en Matemáticas, la mayoría de las cantidades no son conocidas exactamente (salvo que se trate de f...) |
(→Introducción) |
||
| Línea 12: | Línea 12: | ||
de | de | ||
| - | <math>G = \frac{1}{R} = 0.3\,\mathrm{S}</math> | + | <center><math>G = \frac{1}{R} = 0.3\,\mathrm{S}</math></center> |
sería probablemente más correcto. | sería probablemente más correcto. | ||
[[Categoría:Prácticas de laboratorio]] | [[Categoría:Prácticas de laboratorio]] | ||
Revisión de 10:41 18 mar 2010
Introducción
En Ingeniería y en las Ciencias Experimentales, a diferencia de en Matemáticas, la mayoría de las cantidades no son conocidas exactamente (salvo que se trate de factores numéricos como 2, 10 o π). Los datos y resultados de cálculos físicos proceden en última instancia de la experiencia y por tanto están sujetos a incertidumbre.
Así, por ejemplo, la aceleración de la gravedad en la superficie terrestre no es exactamente 
sino una cantidad que varía de punto a punto y cuyo valor conocido está limitado por la precisión de los aparatos experimentales empleados para medirla.
Por esta razón, en Ingeniería o Física no existen las cantidades con infinitos decimales, ya que esto implicaría un conocimiento perfecto de un dato experimental. Esto quiere decir que si medimos, por ejemplo, una resistencia y obtenemos un valor de aproximadamente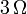 
, y queremos hallar la conductancia, su valor no puede ser
ya que esto significaría que conocemos todos los decimales de la inversa, aun cuando la cantidad original era solo aproximada. Un valor de
sería probablemente más correcto.
