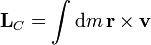Momento cinético de una barra
De Laplace
(Diferencias entre revisiones)
(→Rotación en torno al centro) |
(→Rotación en torno al centro) |
||
| Línea 12: | Línea 12: | ||
El momento cinético respecto al centro será, para una distribución continua | El momento cinético respecto al centro será, para una distribución continua | ||
| - | <center><math>\mathbf{L}_C=\int \mathrm{d}m\mathbf{r}\times\mathbf{v}</math></center> | + | <center><math>\mathbf{L}_C=\int \mathrm{d}m\,\mathbf{r}\times\mathbf{v}</math></center> |
==Rotación en torno a un extremo== | ==Rotación en torno a un extremo== | ||
==Variación de la longitud== | ==Variación de la longitud== | ||
[[Categoría:Problemas de dinámica de un sistema de partículas]] | [[Categoría:Problemas de dinámica de un sistema de partículas]] | ||
Revisión de 21:19 1 mar 2010
Contenido |
1 Enunciado
Una barra homogénea de masa m y longitud L gira en torno a un eje perpendicular a ella y que pasa
por su centro, con velocidad angular uniforme  .
.
- Calcula el momento angular de la barra respecto a su punto central.
- Ahora el eje de giro pasa por uno de sus extremos. Calcula el momento angular de la barra en este caso, respecto a un punto del eje de giro.
- En la situación anterior, la longitud de la barra se multiplica por dos, mientras que su masa permanece constante. ¿Cómo cambia la velocidad angular? ¿Y si se divide por dos?
2 Rotación en torno al centro
Tomamos un sistema de ejes fijos en el cual el origen de coordenadas es el centro de la barra, el eje Z es el eje instantáneo de rotación y X es el eje a lo largo de la barra.
El momento cinético respecto al centro será, para una distribución continua