Ejemplo de un sistema de partículas
De Laplace
(→Aceleración de cada partícula) |
(→Aceleración de cada partícula) |
||
| Línea 67: | Línea 67: | ||
===Aceleración de cada partícula=== | ===Aceleración de cada partícula=== | ||
| - | Dividiendo por la masa de cada | + | Dividiendo la fuerza sobre cada partícula por la masa de cada una obtenemos su aceleración: |
<center> | <center> | ||
| Línea 75: | Línea 75: | ||
! <math>m_i</math> (kg) | ! <math>m_i</math> (kg) | ||
! <math>\mathbf{F}_i</math> (m) | ! <math>\mathbf{F}_i</math> (m) | ||
| - | ! <math>\mathbf{a}_i | + | ! <math>\mathbf{a}_i</math> (m/s<sup>2</sup>) |
|- | |- | ||
| 1 | | 1 | ||
Revisión de 18:04 28 feb 2010
Contenido |
1 Enunciado
Tres partículas puntuales se encuentran en un cierto instante en los vértices de un triángulo. Las masas, posiciones y velocidades de las partículas son, en el SI,
| i | mi (kg) | 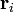 (m) (m)
| 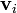 (m/s) (m/s)
|
|---|---|---|---|
| 1 | 5 | 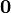
| 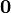
|
| 2 | 4 | 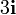
| 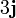
|
| 3 | 3 | 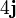
| 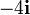
|
Las tres partículas están conectadas por resortes con la misma constante k = 30N / m y longitud natural nula. No hay más fuerzas actuando en el sistema. Para el instante indicado:
- Determina la aceleración de cada partícula.
- Calcula la posición, velocidad y aceleración del CM.
- Calcula el momento cinético del sistema respecto al origen y respecto al CM.
- Halla la energía cinética del sistema respecto al origen y respecto al CM.
- Calcula las derivadas respecto al tiempo de la cantidad de movimiento, del momento cinético y de la energía cinética.
2 Aceleraciones
La aceleración de cada partícula la hallamos dividiendo la fuerza que actúa sobre la partícula entre su masa
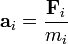
2.1 Fuerza sobre cada partícula
La fuerza sobre una partícula situada en un punto B debida a un oscilador armónico cuyo otro extremo se encuentra en un punto A es
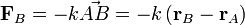
La fuerza sobre la partícula A, de acuerdo con la 3ª ley de Newton, es igual y de sentido contrario a esta.
En este caso, que cada partícula está sujeta a dos muelles, la fuerza sobre una de ella será la resultante de dos fuerzas como la anterior. Para la partícula 1, en el SI,
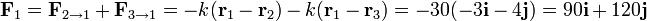
donde hemos tenido en cuenta que las dos constantes de los resortes son iguales a 30 N/m.
Operando del mismo modo para la partícula 2
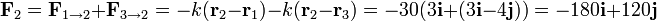
y para la partícula 3
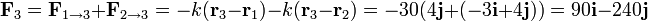
Por tratarse de fuerzas internas, la suma de ellas es nula
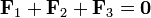
2.2 Aceleración de cada partícula
Dividiendo la fuerza sobre cada partícula por la masa de cada una obtenemos su aceleración:
| i | mi (kg) | 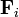 (m) (m)
| 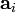 (m/s2) (m/s2)
|
|---|---|---|---|
| 1 | 5 | 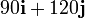
| 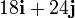
|
| 2 | 4 | 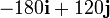
| 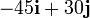
|
| 3 | 3 | 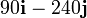
| 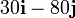
|





