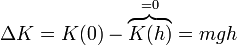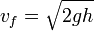Teorema de las fuerzas vivas
De Laplace
(→Teorema de la fuerzas vivas) |
(→Teorema de la fuerzas vivas) |
||
| Línea 34: | Línea 34: | ||
Este teorema implica, entre otras resultados, que una partícula sometida a una fuerza puramente normal en todo momento (como es la fuerza magnética <math>\mathbf{F}=q\mathbf{v}\times\mathbf{B}</math>) mantiene constante su energía cinética y por tanto se mueve de manera uniforme (aunque la dirección de movimiento sea cambiante). | Este teorema implica, entre otras resultados, que una partícula sometida a una fuerza puramente normal en todo momento (como es la fuerza magnética <math>\mathbf{F}=q\mathbf{v}\times\mathbf{B}</math>) mantiene constante su energía cinética y por tanto se mueve de manera uniforme (aunque la dirección de movimiento sea cambiante). | ||
| + | |||
| + | ==Ejemplos== | ||
| + | ===Trabajo realizado por el peso=== | ||
| + | Supongamos una partícula que cae por acción de la gravedad desde una altura <math>h</math> hasta el suelo. Se trata de averiguar con que velocidad impacta con el suelo si inicialmente estaba en reposo. Una posibilidad es, por supuesto, emplear la solución del problema como función del tiempo, pero no es necesario. | ||
| + | |||
| + | El trabajo realizado por el peso es la integral | ||
| + | |||
| + | <center><math>W_{h\to 0}=\int_h^0 (-mg\mathbf{k})\cdot(\mathrm{d}z\mathbf{k}}= -\int_h^0 mg\,\mathrm{d}z = mgh</math></center> | ||
| + | |||
| + | Este trabajo es igual al incremento de energía cinética. Puesto que la energía cinética inicial es nula, este valor es igual a la energía final | ||
| + | |||
| + | <center><math>\Delta K = K(0) - \overbrace{K(h)}^{=0} = mgh</math> {{tose}} <math>\frac{1}{2}mv_f^2 = mgh</math> {{tose}} <math>v_f = \sqrt{2gh}</math></center> | ||
| + | |||
[[Categoría:Introducción a la dinámica]] | [[Categoría:Introducción a la dinámica]] | ||
Revisión de 17:44 15 feb 2010
Contenido |
1 Trabajo y potencia
Se define el trabajo elemental realizado por una fuerza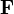 
sobre una partícula que realiza un desplazamiento diferencial 
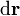como la cantidad escalar
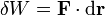
A partir de aquí obtenemos el trabajo realizado sobre una partícula que se mueve desde un punto A a un punto B recorriendo una curva C como la suma de los trabajos elementales a lo largo de dicha curva
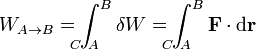
Igualmente, se define la potencia desarrollada por la fuerza como el trabajo que realiza durante un tiempo dt, dividido por dicho intervalo
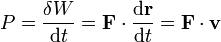
2 Teorema de la fuerzas vivas
Aplicando la segunda ley de Newton la potencia desarrollada por una fuerza puede escribirse como la derivada respecto al tiempo de la energía cinética
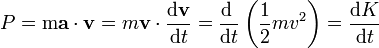
siendo K la energía cinética de la partícula
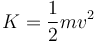
(donde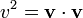 
es el módulo de la velocidad, o celeridad, al cuadrado).
Integrando respecto al tiempo obtenemos el teorema de las fuerzas vivas (o teorema trabajo-energía cinética):
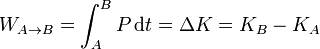
En palabras:
- “El trabajo realizado sobre una partícula entre dos puntos equivale al incremento de la energía cinética de dicha partícula.”
El trabajo realizado no tiene por qué ser necesariamente positivo. Si la partícula se ve frenada, su energía cinética disminuye y el trabajo resultante es negativo.
Este teorema implica, entre otras resultados, que una partícula sometida a una fuerza puramente normal en todo momento (como es la fuerza magnética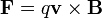 
) mantiene constante su energía cinética y por tanto se mueve de manera uniforme (aunque la dirección de movimiento sea cambiante).
3 Ejemplos
3.1 Trabajo realizado por el peso
Supongamos una partícula que cae por acción de la gravedad desde una altura h hasta el suelo. Se trata de averiguar con que velocidad impacta con el suelo si inicialmente estaba en reposo. Una posibilidad es, por supuesto, emplear la solución del problema como función del tiempo, pero no es necesario.
El trabajo realizado por el peso es la integral
Este trabajo es igual al incremento de energía cinética. Puesto que la energía cinética inicial es nula, este valor es igual a la energía final
